Дуопризма
| Множество однородных p, q-дуопризм | |
| Type | Призматический однородный четырёхмерный многогранник[англ.] |
| Символ Шлефли | {p}×{q} |
| Диаграмма Коксетера — Дынкина | |
| Ячейки | p q-угольных призм, q p-угольных призм |
| Грани | pq квадратов, p q-угольников, q p-угольников |
| Рёбра | 2pq |
| Вершины | pq |
| Вершинная фигура |  Равногранный тетраэдр |
| Симметрия[англ.] | [p,2,q], order 4pq |
| Двойственный | p, q-Дуопирамида[англ.] |
| Свойства | выпуклый, вершинно однородный |
| Множество однородных p, p-дуопризм | |
| Тип | Призматический однородный четырёхмерный многогранник[англ.] |
| Символ Шлефли | {p}×{p} |
| Диаграмма Коксетера — Дынкина | |
| Ячейки | 2p p-gonal prisms |
| Грани | p2 squares, 2p p-gons |
| Рёбра | 2p2 |
| Вершины | p2 |
| Нотация Коксетера[англ.] | [[p,2,p]] = [2p,2+,2p], order 8p2 |
| Двойственный | p, p-Дуопирамида[англ.] |
| Properties | выпуклый, вершинно однородный, фасет-транзитивный[англ.] |
Дуопризма — многогранник, полученный прямым произведением двух многогранников, каждое размерности два и выше. Прямое произведение n-многогранника и m-многогранника — это (n+m)-многогранник, где n и m не меньше 2 (многоугольник или многогранник).
Дуопризмы наименьшей размерности существуют в 4-мерном пространстве как 4-мерные многогранники, будучи прямым произведением двух многоугольников в 2-мерном евклидовом пространстве. Точнее, это множество точек:
- ,
где P1 и P2 — два множества точек, расположенные в многоугольниках (сомножителях). Если оба многоугольника выпуклы, такая дуопризма выпукла и ограничена призматическими ячейками.
Терминология[править | править код]
Четырёхмерные дуопризмы считаются призматическими 4-мерными многогранниками. Дуопризма, полученная произведением двух правильных многоугольников с той же самой длиной рёбер, называется однородной дуопризмой.
Дуопризма, полученная из n-многоугольника и m-многоугольника, называется добавлением «дуопризма» после имён базовых многоугольников, например, треугольно-пятиугольная дуопризма — это произведение треугольника и пятиугольника.
Альтернативный путь именования — это добавление префикса с указанием числа сторон базовых многоугольников, например, 3,5-дуопризма — это треугольно-пятиугольная дуопризма.
Другие альтернативные имена:
- q-угольно-p-угольная призма
- q-угольно-p-угольная двойная призма
- q-угольно-p-угольная гиперпризма
Термин дуопризма был введён Джорджем Ольшевски как сокращение от double prism (двойная призма). Джон Хортон Конвей предложил похожее имя proprism как сокращение от product prism (произведение призм). Дуопризмы являются пропризмами, образованные произведением в точности двух многогранников.
Пример 16,16-дуопризмы[править | править код]
Диаграмма Шлегеля Показана проекция из центра одной 16-угольной призмы и все, кроме одной, противоположные 16-угольные призмы. |
Развёртка Показаны два множества 16-угольных призм. Верхняя и нижняя грани вертикального цилиндра соединены в четырёхмерном пространстве. |
Геометрия 4-мерных дуопризм[править | править код]

4-мерная однородная[англ.] дуопризма получается произведение правильного n-стороннего многоугольника и правильного m-стороннего многоугольника с одинаковыми длинами сторон. Она ограничена n m-угольными призмами и m n-угольными призмами. Например, прямое произведение треугольника и шестиугольника — это дуопризма, ограниченная шестью треугольными призмами и тремя шестиугольными.
- Если m и n идентичны, результирующая дуопризма ограничена 2n одинаковыми n-угольными призмами. Например, прямое произведение двух треугольников — это дуопризма, ограниченная шестью треугольными 6 призмами.
- Если m иn равны 4, результирующая дуопризма ограничена восемью квадратными призмами (кубами) и идентична тессеракту.
m-угольные призмы соединены друг с другом m-угольными гранями и образуют замкнутый цикл. Подобным обрразом n-угольные призмы соединены друг с другом n-угольными гранями и образуют другой замкнутый цикл, перпендикулярный первому. Эти два цикла соединены друг с другом через их квадратные грани и взаимно перпендикулярны.
При стремлении m и n к бесконечности соответствующие дуопризмы приближаются к дуоцилиндру[англ.]. Таким образом, дуопризмы полезны как неквадратичные приближения к дуоцилиндрам.
Развёртки[править | править код]
 3-3[англ.] |
 4-4[англ.] |
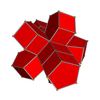 5-5 |
 6-6[англ.] |
 8-8[англ.] |
 10-10[англ.] |
 3-4 |
 3-5[англ.] |
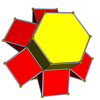 3-6[англ.] |
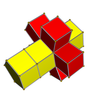 4-5[англ.] |
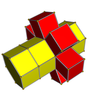 4-6[англ.] |
 3-8[англ.] |
Перспективные проекции[править | править код]
Центрированная относительно ячейки перспективная проекция дуопризмы выглядит как тор с двумя множествами ортогональных ячеек, p-угольных и q-угольных призм.

|

|
| 6-призма | 6,6-дуопризма[англ.] |
|---|---|
| Шестиугольная призма, спроецированная перспективно на плоскость и центрированная относительно шестиугольной грани, выглядит как два шестиугольника, соединённые (деформированными) квадратами. Подобным же образом проекция 6,6-дуопризмы в трёхмерное пространство близка тору, шестиугольному как в плоскости, так и в сечении. | |
(p, q)-дуопризмы идентичны (q, p)-призмам, но в проекциях выглядит различными, поскольку центрированы относительно различных ячеек.
 3-3[англ.] |
 3-4 |
 3-5[англ.] |
 3-6[англ.] |
 3-7[англ.] |
 3-8[англ.] |
 4-3 |
 4-4[англ.] |
 4-5[англ.] |
 4-6[англ.] |
 4-7 |
 4-8[англ.] |
 5-3[англ.] |
 5-4 |
 5-5 |
 5-6 |
 5-7 |
 5-8 |
 6-3[англ.] |
 6-4[англ.] |
 6-5 |
 6-6[англ.] |
 6-7 |
 6-8[англ.] |
 7-3 |
 7-4 |
 7-5 |
 7-6 |
 7-7 |
 7-8 |
 8-3[англ.] |
 8-4[англ.] |
 8-5 |
 8-6[англ.] |
 8-7 |
 8-8[англ.] |
Ортогональные проекции[править | править код]
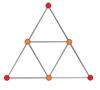
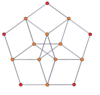
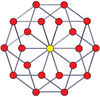
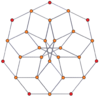
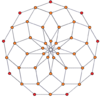
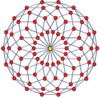
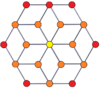
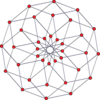
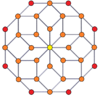
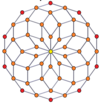
Вершинно-центрированные ортогональные проекции p, p-дуопризм имеет симметрию [2n] для нечётных значений и [n] для чётных, при этом n вершин проецируется в центр. Для 4,4 это представляет плоскость Коксетера A3 тессеракта. Проекция 5,5 идентична трёхмерному ромботриаконтаэдру.
| Нечётные | |||||||
|---|---|---|---|---|---|---|---|
| 3-3[англ.] | 5-5 | 7-7 | 9-9 | ||||
 |

|
 |
|
 |

|
 |
|
| [3] | [6] | [5] | [10] | [7] | [14] | [9] | [18] |
| Чётные | |||||||
| 4-4[англ.] (тессеракт) | 6-6[англ.] | 8-8[англ.] | 10-10[англ.] | ||||
 |

|
 |
|
 |

|
 |

|
| [4] | [8] | [6] | [12] | [8] | [16] | [10] | [20] |
Связанные многогранники[править | править код]

Правильный косой многогранник, {4,4|n}, существует в 4-мерном пространстве как n2 квадратных граней n-n дуопризмы, использующий все 2n2 рёбер и n2 вершин. 2n n-угольные грани можно рассматривать как удалённые. (Косые многогранники можно рассматривать таким же образом как n-m дуопризмы, но они не являются правильными.)[1]
Дуоантипризма[править | править код]


Подобно антипризмам как альтернированным призмам существует множество 4-мерных дуоантипризм — это 4-многогранники, которые можно создать операцией альтернации[англ.], применённой к дуопризме. Альтернированные вершины создают неправильные тетраэдральные ячейки, за исключением специального случая дуопризмы 4-4 (тессеракта), при которой получается однородный (и правильный) шестнадцатиячейник. Шестнадцатиячейник является единственной однородной дуоантипризмой.
Дуопризмы ![]()
![]()
![]()
![]()
![]()
![]()
![]() , t0,1,2,3{p,2,q}, могут быть альтернированы в
, t0,1,2,3{p,2,q}, могут быть альтернированы в ![]()
![]()
![]()
![]()
![]()
![]()
![]() , ht0,1,2,3{p,2,q}, «дуоантипризмы», которые нельзя получить однородными. Единственное выпуклое однородное решение — тривиальный случай p=q=2, который является наименьшей по симметрии конструкцией тессеракта
, ht0,1,2,3{p,2,q}, «дуоантипризмы», которые нельзя получить однородными. Единственное выпуклое однородное решение — тривиальный случай p=q=2, который является наименьшей по симметрии конструкцией тессеракта ![]()
![]()
![]()
![]()
![]()
![]()
![]() , t0,1,2,3{2,2,2}, с альтернированием в шестнадцатиячейник,
, t0,1,2,3{2,2,2}, с альтернированием в шестнадцатиячейник, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , s{2}s{2}.
, s{2}s{2}.
Единственное невыпуклое однородное решение — p=5, q=5/3, ht0,1,2,3{5,2,5/3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , полученное из 10 пятиугольных антипризм, 10 пентаграммных скрещенных антипризм[англ.] и 50 тетраэдов. Этот многогранник известен под именем большая дуоантипризма[англ.][2][3].
, полученное из 10 пятиугольных антипризм, 10 пентаграммных скрещенных антипризм[англ.] и 50 тетраэдов. Этот многогранник известен под именем большая дуоантипризма[англ.][2][3].
Многогранники k22[править | править код]
3,3-дуопризма[англ.], −122, является первой в серии размерностей однородных многогранников, обозначенных Коксетером как серия k22. 3,3-дуопризма является вершинной фигурой второй фигуры, биспрямлённого 5-симплекса[англ.]. Четвёртой фигурой являются евклидовы соты, 222[англ.] Последней фигурой являются паракомпактные гиперболические соты, 322, с группой Коксетера [32,2,3], . Каждый последующий однородный многогранник строится из предыдущего (предыдущий служит его вершинной фигурой).
| k21[англ.] в пространстве размерности n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пространство | Конечное | Евклидово | Гиперболическое | ||||||||
| En[англ.] | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Группа Коксетера |
E₃=A₂A₁ | E₄=A₄ | E₅=D₅ | E₆ | E₇[англ.] | E₈ | E₉ = Ẽ₈ = E₈+ | E₁₀ = T₈ = E₈++ | |||
| Диаграмма Коксетера |
|||||||||||
| Симметрия[англ.] | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Порядок | 12 | 120 | 192 | 51 840 | 2 903 040 | 696 729 600 | ∞ | ||||
| Граф | 
|

|

|

|

|

|
- | - | |||
| Обозначение | −121 | 021 | 121 | 221[англ.] | 321[англ.] | 421[англ.] | 521[англ.] | 621[англ.] | |||
См. также[править | править код]
- Многогранник и Четырёхмерный многогранник
- Выпуклый правильный четырёхмерный многогранник[англ.]
- Дуоцилиндр[англ.]
- Тессеракт
Примечания[править | править код]
- ↑ В английской литературе skew polyhedron (косой многогранник) соответствует трёхмерной фигуре, для которой в русском языке прижился термин косой многоугольник. Термин skew polytop (косой политоп) соответствует многомерной (размерность больше трёх) фигуре. В данной статье используется термин косой многогранник для всех размерностей.
- ↑ Jonathan Bowers — Miscellaneous Uniform Polychora Архивная копия от 24 сентября 2015 на Wayback Machine 965. Gudap
- ↑ http://www.polychora.com/12GudapsMovie.gif Архивная копия от 22 февраля 2014 на Wayback Machine Animation of cross sections
Литература[править | править код]
- H. S. M. Coxeter. Regular Polytopes[англ.]. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — С. 124. — ISBN 0-486-61480-8.
- H.S.M. Coxeter. The Beauty of Geometry: Twelve Essays. — 1999. — ISBN 0-486-40919-8.
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
- Henry P. Manning. The Fourth Dimension Simply Explained. — New York: Munn & Company, 1910.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. (Chapter 26) // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- Norman Johnson. Uniform Polytopes. — Manuscript, 1991.
- Norman Johnson. The Theory of Uniform Polytopes and Honeycombs. — Ph.D. Dissertation. — University of Toronto, 1966.
- George Olshevsky[англ.] Duoprism на Glossary for Hyperspace
- George Olshevsky[англ.] Cartesian product на Glossary for Hyperspace
- Каталог выпуклых многогранников George Olshevsky[англ.]
Ссылки[править | править код]
- The Fourth Dimension Simply Explained—describes duoprisms as «double prisms» and duocylinders as «double cylinders»
- Polygloss — glossary of higher-dimensional terms
- Exploring Hyperspace with the Geometric Product
Для улучшения этой статьи желательно:
|

