Обсуждение:Комплексное число

Рецензирование статьи Комплексное число

Здесь находятся завершившиеся обсуждения. Просьба не вносить изменений.

В 2013 году на СО статьи долго обсуждалось её печальное состояние и возможные пути доработки, но затем дело заглохло. Теперь я решил ликвидировать старый долг, существенно переработал и дополнил эту важнейшую статью с учётом сделанных на СО замечаний. Несколько недостающих сносок скоро добавлю. Жду новых замечаний. LGB (обс.) 12:58, 13 января 2018 (UTC)`

• Не уверен нужна ли, но, всё же, отсутсвует ссылка на "зарубежные источники, в которых встречаются готические символы обозначений вещественной и мнимой частей". Trevanpwrd (обс.) 03:06, 16 января 2018 (UTC +3)`
  • Вообще-то само существование готических Tex-символов \Re, \Im достаточно убеждает, но для порядка вставил две сноски на уважаемый сайт mathworld.wolfram.com. LGB (обс.) 11:29, 16 января 2018 (UTC)
• В разделе "Комплексная плоскость" обозначения на картинке (a и b) не соответствуют обозначениям в тексте (x и y). Лучше поменять картинку например на File:Simple illustration of a complex number.svg. — Алексей Копылов 08:13, 16 января 2018 (UTC)
  • Спасибо, Сделано. LGB (обс.) 11:29, 16 января 2018 (UTC)
• Кстати, я бы эту картинку использовал и в преамбуле, а то буква вместо картинки не информативна. — Алексей Копылов 08:13, 16 января 2018 (UTC)
  • В преамбуле эту картинку, по-моему, рано, потому что тогда придётся разъяснять детали геометрического представления. LGB (обс.) 12:13, 16 января 2018 (UTC)
    • По-моему, не обязательно. Это ж только иллюстрация. К тому же большинство читающих эту статью имеют представление о комплексных числах. Впрочем это дело вкуса. — Алексей Копылов 03:45, 17 января 2018 (UTC)
      • Ну, если у читателя уже есть представление, то ему картинка и не нужна. А если нет, то она может создать неправильное представление о сущности комплексных чисел (я когда-то спорил на эту тему на СО в 2013-м). Исторически и логически комплексные числа — это алгебраическое понятие, геометрическая модель возникла только в XIX веке. Поэтому начало статьи не выходит за пределы алгебры. Обсуждаемая картинка может навести на мысль, что «комплексное число — это точка» (или вектор), что по существу неверно. Возможно, я преувеличиваю важность этого момента (существуют даже учебники, которые определяют комплексное число как точку или пару чисел), но методически и эстетически считаю правильным начать с чистой алгебры. LGB (обс.) 10:54, 17 января 2018 (UTC)
        • Понятно. — Алексей Копылов 16:58, 17 января 2018 (UTC)
    • Кстати, французы используют картинку с множеством Мандельброта. При этом в тексте у них про Мандельброта ничего нет. Может нам тоже использовать эту картинку в разделе комплексной плоскости или даже в преамбуле? Для раскрытия темы это не важно, но просто для красоты. — Алексей Копылов 03:56, 17 января 2018 (UTC)
      • Заклюют за нарушение правила Википедия:Иллюстрирование . LGB (обс.) 10:54, 17 января 2018 (UTC)
• Нет формулы arg(z_1 z_2) = arg (z_1) + arg(z_2) — Алексей Копылов 08:13, 16 января 2018 (UTC)
  • В предыдущем разделе сказано, что «при перемножении комплексных чисел их модули перемножаются, а аргументы складываются». Но привести формулу тоже не вредно, вставил. LGB (обс.) 12:13, 16 января 2018 (UTC)
• "так же как сомнительными в то время считали и иррациональные числа". Разве иррациональные числа считали сомнительными? — Алексей Копылов 08:13, 16 января 2018 (UTC)
  • Вообще-то считали, см. История математики, том 1, стр. 304. Но эта информация не имеет прямого отношения к теме статьи, так что я её укоротил. LGB (обс.) 12:13, 16 января 2018 (UTC)

• Я бы историю всё-таки вверх поднял. А то как учебник начинается. - DZ - 23:52, 25 января 2018 (UTC)
  • В разделе История упоминаются некоторые тематические понятия, например, геометрическое представление комплексных чисел и формула Муавра. Поэтому естественно поместить Историю после разделов, где введены эти понятия. А тогда другого выбора нет. Кстати, в английском и немецком разделе История вообще в самом конце. А вы где конкретно предлагаете поместить этот раздел? LGB (обс.) 10:51, 26 января 2018 (UTC)
    • Я бы с него начал. А на термины, для которых есть отдельные статьи, у нас вроде как принято ссылки делать. Для внутренних можно тоже ссылку на раздел сделать, если что-то совсем неочевидное. Но я не настаиваю. - DZ - 11:09, 26 января 2018 (UTC)
      • Ну, пусть сообщество выскажется. LGB (обс.) 11:11, 26 января 2018 (UTC)
        • В середине между чисто математическими разделами этот раздел действительно теряется. Я бы перенес его либо в начало (не страшно, что некоторые определения идут после, для общего понимания это не важно). Либо наоборот в самый конец (возможно перед "Вариации и обобщения"). — Алексей Копылов 10:39, 27 января 2018 (UTC)
• Предлагаю добавить шаблон main где возможно, а то квантовая механика выглядит сиротливо. Alexander Mayorov (обс.) 04:22, 28 января 2018 (UTC)
  • Можно и добавить, но вообще-то там уже в первом предложении есть ссылка на статью Квантовая механика. А где ещё вы считаете полезным добавить Main? LGB (обс.) 11:12, 28 января 2018 (UTC)
    • Везде где есть статья раскрывающая содержпние подраздела более полно. Математика точно должна быть, конформное отображение, комплексная плоскость. Alexander Mayorov (обс.) 13:21, 28 января 2018 (UTC)
• Не нравится содержание преамбулы. Там должно быть краткое содержание статьи. Возможно добавить ссылки на внутренние разделы. " два комплексных числа нельзя сравнивать на больше/меньше." не понять о чём речь, потому что сравнивать числа можно и по амплитуде и по фазе, ну в электротехнике не гнушаются. Неравенство треугольника -- такое сравнение по модулю, например. Если комплексные числа нащли применение в картографии, то наверное надо написать в чём именно или не упоминать в преамбуле -- тема не раскрыта этого самого применения. В преамбуле не отражены большие разделы как например аксиоматика, геометрия тригонометрия. Я бы сдвинул раздел истории в самое начало, так как она явно интереснее написана чем арифметика. Alexander Mayorov (обс.) 13:21, 28 января 2018 (UTC)
  • Я добавил сносок про картографию в раздел о практическом применении. Там пояснено, что причиной использования комплексной модели в картографии является гибкость настройки преобразования комплексной плоскости на желаемый тип построения карты. Теперь объясню, почему так выбрано расположение раздела История. Я всюду стараюсь разместить материал по возрастанию сложности, чтобы читатель при последовательном чтении не упустил ничего доступного для его текущего уровня. Если поместить Историю ниже, где материал для продвинутого читателя, начинающие до неё просто не доберутся, хотя она вполне доступна по уровню. Если, наоборот, сдвинуть выше, то у тех читателей, которые заинтересованы получить первичное ознакомление с предметом, нарушится логический порядок материала, и они могут прекратить чтение преждевременно. LGB (обс.) 11:50, 29 января 2018 (UTC)

• За последний день статья сильно улучшилась, но у меня появились новые замечания:
  • "Аксиоматика комплексных чисел была построена трудами Кэли, Фробениуса". Сомнительно. В тексте этого нет, и источники не указаны. Alexander Mayorov возможно вы что-то другое имели в виду? — Алексей Копылов 09:16, 29 января 2018 (UTC)
    • Не знаю, чесно говоря, кто придумал аксиоматику в таком виде. Но она отличается от этой. Я хотел бы видеть фразу в этом виде, но если действительно это неизвестно, то лучше что-нибудь другое написать. Alexander Mayorov (обс.) 11:14, 29 января 2018 (UTC)
      • Фробениус в статье упоминается, а Кэли, пожалуй, уберу. Взамен добавил пионера этой темы — Гамильтона. LGB (обс.) 11:50, 29 января 2018 (UTC)
        • Упоминается, но не в той части, на которую ведет ссылка. Теорема Фробениуса - это не построение аксиоматики, и Гамильтон (судя по тексту) строил не аксиоматику, а модель. Вместо этого лучше объединить эту фразу со следующей и сказать, что Гамильтон, Фробениус и Кэли рассмотрели прочие возможные расширения действительных чисел. Но у меня нет под рукой АИ, чтобы проверить, что это не ОРИСС. — Алексей Копылов 02:38, 30 января 2018 (UTC)
          • Я покопался в своей библиотеке, но внятной информации, кто первый предложил аксиоматику комплексных чисел, не нашёл. Поэтому переделал спорную фразу: «Непротиворечивость системы комплексных чисел была доказана построением их строгой аксиоматики». О расширениях C рассказано в отдельном разделе, о теореме Фробениуса также сказано, а в преамбуле, по-моему, достаточно краткого упоминания. LGB (обс.) 10:45, 30 января 2018 (UTC)
            • Это неверно: непротиворечивость доказывается построением модели, а не аксиоматики. Аксиоматика комплексных чисел не такая уж важная вещь, можно про нее в преамбуле не говорить. См. также мои новые замечания по разделу "Логические основания" ниже.
            • Всякая модель опирается на (не всегда явную) аксиоматику свойств, иначе как проверить её адекватность? И мне не хотелось в самом начале упоминать такие неочевидные термины, как модели. Решил перенести фразу в укороченном виде повыше. LGB (обс.) 11:02, 31 января 2018 (UTC)

• • Раз теперь про геометрическую интерпретацию есть в преамбуле (что на мой взгляд правильно), предлагаю все-таки поставить в преамбулу картинку с комплексной плоскостью. — Алексей Копылов 09:16, 29 января 2018 (UTC)
    • Уговорили, добавил. LGB (обс.) 11:50, 29 января 2018 (UTC)
      • Я бы еще картинку с С убрал. — Алексей Копылов 02:38, 30 января 2018 (UTC)
        • Я её поместил по аналогии со статьёй Целое число. Хотя там она симпатичнее. Заменил картинку, посмотрите, так лучше? LGB (обс.) 10:45, 30 января 2018 (UTC)
          • По-моему, хуже. Раньше хоть $\mathbb {C}$ была. Тогда уж так:

<div style="float:right; margin: 0 0 0 0.2em; font-size: 500%; "><math>\mathbb{C}</math></div> →

$\mathbb {C}$

Хотя, по-моему, это ни к чему. Если вы хотите показать, что алгебраическая интерпретация более первична, чем геометрическая, можно так:

<div style="float:right; width: 220px; text-align: center; font-size: 300%; "><math>i^2=-1</math></div>
[[Файл:A plus bi.svg|мини|220px|Геометрическое представление комплексного числа]]

$i^{2}=-1$

Геометрическое представление комплексного числа

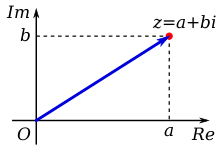
— Алексей Копылов 03:19, 31 января 2018 (UTC)

Последний вариант меня устраивает, заменил. LGB (обс.) 11:02, 31 января 2018 (UTC)

Зачем вообще нужна тривиальная картинка $\mathbb {C}$ причём дублирующая текст статьи? Alexander Mayorov (обс.) 04:48, 31 января 2018 (UTC)

Несколько замечаний:

• 0 это реальное число или мнимое? Из определений не понятно, значит следует уточнить.
  • В разделе «Связанные определения» говорится, что число с нулевой мнимой частью рассматривается как вещественное. LGB (обс.) 10:45, 30 января 2018 (UTC)
• "Уже упоминалось, что комплексные числа нельзя сравнивать на больше/меньше." что за разделить?
  • Это обычный символ «или», неужели он вам никогда не попадался в текстах? См., например, тут. Иногда вместо черты ставят дефис: больше-меньше. Никто до вас не удивлялся этой конструкции. LGB (обс.) 10:45, 30 января 2018 (UTC)
    • Это не на русском языке или. Я пересисал во введении вашу формулировку. "Нельзя указать какое из чисел больше или меньше." "/" - это либо математический символ что означает разделить либо его не должно быть в символах пунктуации. Alexander Mayorov (обс.) 04:48, 31 января 2018 (UTC)
      • Заменил черту на дефис. LGB (обс.) 11:02, 31 января 2018 (UTC)
      • Косая черта применяется в научной речи: Косая черта#Небуквенный орфографический знак. — Алексей Копылов 09:15, 1 февраля 2018 (UTC)

• "Можно сравнивать комплексные числа только на «равно/не равно»" о чём речь что такое равно разделить на не равно
  • То же самое. LGB (обс.) 10:45, 30 января 2018 (UTC)

• "любой многочлен с вещественными или комплексными коэффициентами имеет столько корней какова его степень" Сколько корней у многочлена x^2? корень один, так как одно число соответствует корню.
  • Добавил: «с учётом кратности». LGB (обс.) 10:45, 30 января 2018 (UTC)
• "Дополнительные отличия имеют функции комплексного переменного." источник?
  • В тексте стоит ссылка на нижележащий раздел, все источники там приведены. LGB (обс.) 10:45, 30 января 2018 (UTC)
    • Кстати, (на мой вкус) ссылки на раздел в той же статье лучше оформлять при помощи шаблонов {{переход}}, чтобы читатель сразу понял, что он перейдет не в другую статью, а в раздел той же самой. Если вам не нравятся стрелочки, то можно написать словами (см. [[#Комплексные функции|ниже]]) → (см. ниже).
      • По-моему лишнии слова "ниже", "см. также" излишни. Если нужно перейти в другую страницы то используют гиперссылки для терминов. Alexander Mayorov (обс.) 04:48, 31 января 2018 (UTC)
        • Заменил. LGB (обс.) 11:02, 31 января 2018 (UTC)
• "Замечания" источник?
  • Замечания совершенно тривиальны, а для тривиальной информации, согласно правилам, источник не требуется. LGB (обс.) 10:45, 30 января 2018 (UTC)
    • Не все замечания тривиальны. Например, "вплоть до конца XIX века второй вариант записи считался допустимым" требует источника. Кроме того надо сказать, что квадратный корень может использоваться для обозначения многозначной функции, например как тут: Квадратный корень#Комплексные числа. Кстати, многозначные функции играют важную роль в комплексном анализе, поэтому стоит хотя бы упомянуть их и в Комплексное число#Аналитические функции. — Алексей Копылов 03:19, 31 января 2018 (UTC)
      • В самом деле до конца XIX века (см. пример Куммера в статье Наибольший общий делитель), но источник сходу не нашёл, сформулировал пока нейтрально: «долгое время». О многозначных функциях тут говорить сложно, тогда придётся затрагивать такие непростые темы, как риманова поверхность, объём раздела непропорционально возрастёт. По-моему, ссылки на Комплексный анализ достаточно. LGB (обс.) 11:48, 31 января 2018 (UTC)
      • Ага, нашёл примеры в Истории математики, том III. Восстановил ссылку на XIX век. LGB (обс.) 12:02, 31 января 2018 (UTC)
    • Это нетривиальное замечание поскольку если правильно использовать корни то никакой ошибки не возникает: Alexander Mayorov (обс.) 05:02, 31 января 2018 (UTC)

${\sqrt {-3}}\cdot {\sqrt {-3}}={\sqrt {\left(-3\right)\cdot \left(-3\right)}}={\sqrt {\left(-3\right)^{2}}}={\sqrt {\left(-1\right)^{2}\left(3\right)^{2}}}={\sqrt {\left(-1\right)^{2}}}3=(-1)^{2\cdot 1/2}3=(-1)^{1}3=-3$.

• • • • Есть только один способ правильно использовать корни — не использовать отрицательные числа под знаком радикала. Вы не учли, что знак радикала обычно обозначает арифметический корень. Можете привес ти ссылку на АИ для приведенной вами методики? LGB (обс.) 11:48, 31 января 2018 (UTC)

• "sin,cos — функции косинуса и синуса" это не функции, функция это sin(z) и позже sgn тоже не функция без аргумента. Alexander Mayorov (обс.) 05:51, 30 января 2018 (UTC)
  • sin — это как раз идентификатор функции, а sin(z) — её значение. Часто это отличие подчёркивают записью вроде sin: R -> R. Идентификатор функции как таковой не требует идентификатора аргумента. LGB (обс.) 10:45, 30 января 2018 (UTC)
• Кстати почему ноль комплексный не определён как $0+i0$, если в определении говорится о виде $a+ib$? Alexander Mayorov (обс.) 08:19, 30 января 2018 (UTC)
  • Вы правы, добавил для ясности фразу: «Вместо $a+0i$ обычно пишут просто $a$». LGB (обс.) 10:45, 30 января 2018 (UTC)
    • Нужно добавить также про деление на ноль, а то может можно делить в каких-то случаях? Alexander Mayorov (обс.) 04:48, 31 января 2018 (UTC)
      • В разделе «Деление» дважды говорится, что на нуль делить нельзя. LGB (обс.) 11:48, 31 января 2018 (UTC)

Логические основания

• "Для анализа подобных вопросов надо сформировать набор аксиом для комплексных чисел" - это необязательно. Достаточно построить модель: если мы определим комплексное число, как пару действительных чисел, никаких аксиом нам не нужно, чтобы доказать непротиворечивость или выяснить свойства. Аксиомы нужны, если хочется, например, доказать, что такая модель единственная, или хочется рассуждать о комплексных числах абстрактно без конкретной модели. — Алексей Копылов 03:19, 31 января 2018 (UTC)
  • Я выше уже писал, что модель без аксиоматики бессодержательна. LGB (обс.) 15:22, 31 января 2018 (UTC)
• Матричная модель и модель фактор-кольца многочленов нужны не для того, чтобы доказать непротиворечивость (для этого достаточно стандартной модели), а они интересны сами по себе. Матричная модель показывает, что комплексные числа можно рассматривать как подмножество матриц 2x2, а модель фактор-кольца полезна при рассмотрении других расширений R. Об этом стоит сказать. — Алексей Копылов 03:19, 31 января 2018 (UTC)
  • Раздел как раз и показывает, что комплексные числа можно рассматривать как подмножество матриц 2x2, модель есть модель. Согласен, что это интересно и само по себе. Если вы укажете, где в науке этот факт приносит пользу, то можно и добавить. Прошу сообщить, в каких АИ используется модель фактор-кольца, тоже неплохо бы кратко дополнить. LGB (обс.) 15:22, 31 января 2018 (UTC)
• В связи с этим предлагаю переименовать этот раздел в "Аксиоматика и модели". — Алексей Копылов 03:19, 31 января 2018 (UTC)
  • Какой именно? «Логические основания»? Тогда уж «Аксиоматика, модели и непротиворечивость», так как последняя и является главной целью раздела. А мне кажется, текущее название ничем не хуже. LGB (обс.) 15:22, 31 января 2018 (UTC)
    • @LGB: Прошу прощение, что отвечаю в закрытой секции. Да, «Аксиоматика, модели и непротиворечивость» мне кажеться лучше. — Алексей Копылов 00:34, 25 февраля 2018 (UTC)
      • Давайте обсудим. Перенёс тему на СО статьи. LGB (обс.) 10:47, 25 февраля 2018 (UTC)

Замечаний больше нет, так что выношу на КИС. Всем спасибо.

Аксиоматика комплексных чисел

В аксиоматике следует уточнить информацию, связанную с топологией. Комплексные числа являются нормированным полем. Содержит вещественные числа — это не только «Содержит поле, изоморфное R». Это означает, «содержит поле, изоморфное R, которое линейно упорядочено и является полным топологическим пространством». Mx1024 (обс.) 22:41, 11 февраля 2018 (UTC)

Например, в этом наборе аксиом [1] имеется аксиома о существовании точной верхней грани.Mx1024 (обс.) 22:42, 11 февраля 2018 (UTC)

Аксиоматика приведена согласно классическому построению, описанному у Нечаева, в Энциклопедии элементарной математики и во многих других источниках. Добавлять ОРИСС не имею права. Тем более что подполе C, изоморфное R (имеется ведь в виду не просто изоморфное как множество, а как поле), автоматически индуцирует (допускает перенос) обычного порядка и топологии вещественных чисел и поэтому является полным. Вообще-то поле C содержит бесконечно много подполей, изоморфных R, но для аксиоматики комплексных чисел это неважно. Указанная вами другая версия аксиоматики не содержит аксиомы минимальности и поэтому вынуждена компенсировать её другими аксиомами. LGB (обс.) 10:57, 12 февраля 2018 (UTC)

«Добавлять ОРИСС не имею права» Что вы имеете в виду? Какое утверждение вы называете ориссом? «согласно классическому построению» — да, и я тоже говорю об классическом построении. О каком добавлении орисса вы пишете? «и во многих других источниках» Mx1024 (обс.) 13:53, 12 февраля 2018 (UTC)

Я понял вашу реплику в том смысле, что вы предлагаете заменить в статье аксиому «Содержит поле, изоморфное R» на «содержит поле, изоморфное R, которое линейно упорядочено и является полным топологическим пространством». Вот эта операция была бы ОРИССом. Если вы имели в виду иное, прошу уточнить, что вы конкретно предлагаете и на какие источники опираетесь. LGB (обс.) 14:17, 12 февраля 2018 (UTC)

Это утверждение будет верным или неверным в зависимости от того, как понимать аксиому «поле C содержит R»

Это не означает, что все свойства разных моделей идентичны; например, алгебраическое замыкание поля p-адических чисел {\displaystyle \mathbb {Q} _{p}} {\mathbb {Q}}_{p} удовлетворяет приведенной аксиоматике и поэтому изоморфно {\displaystyle \mathbb {C} } \mathbb {C} как поле, но не изоморфно как топологическое пространство

Алгебраическое замыкание поля p-адических чисел (обозначим его Cp) изоморфно полю C, как полю. Но у них разные нормы. Аксиома «содержит R с обычной нормой» не выполняется для Cp. Mx1024 (обс.) 13:53, 12 февраля 2018 (UTC)

Вполне согласен, это означает, кстати, что и на R можно ввести существенно разные нормы. Может быть, вы хотите сказать, что аксиоматика Нечаева и др. недостаточна для построения полной теории комплексных чисел? Тогда нашей с вами дискуссии недостаточно, для опровержения такого сверхавторитетного источника, как Нечаев, требуется как минимум такой же авторитет. LGB (обс.) 14:17, 12 февраля 2018 (UTC)

Я добавил в раздел об аксиоматике абзац со ссылкой на указанный вами сайт, читателю может быть полезной информация об альтернативных вариантах аксиоматики. Хотя опора на ZFC предполагает более продвинутого читателя, и она сложнее по построению. С другой стороны, в отличие от конструкции в статье, альтернативная аксиоматика хорошо укладывается в стандарты гильбертовской метаматематики. LGB (обс.) 16:35, 13 февраля 2018 (UTC)

Основной вопрос данной темы. Входит или нет в систему аксиом информация о норме и топологии поля C.

Поле С полно относительно (единственной) нормы, продолжающей норму |*| с R. (Коблиц. p-адические числа, ... §3.Как строится поле комплексных чисел, стр.20-21.)

Расширим теперь поле действительных чисел D до поля комплексных чисел K. (Энциклопедия элементарной математики, книга 1, стр.228)

Поле действительных чисел, аксиомы I - XII. (Энциклопедия элементарной математики, книга 1, стр.223-224)

Mx1024 (обс.) 11:45, 14 февраля 2018 (UTC)

Информация о норме и топологии поля C в аксиомы, безусловно, не входит, в этом нет никакой необходимости. Эти структуры строятся независимо и однозначно, исходя из желаемых свойств — в первую очередь, как вы отметили, норма C должна быть продолжением нормы R и иметь аналогичные свойства. LGB (обс.) 12:01, 14 февраля 2018 (UTC)

«Эти структуры строятся независимо и однозначно». Однозначно? См. приведенный выше пример. Алгебраическое замыкание Cp поля p-адических чисел и комплексные числа C с «обычной» нормой. Mx1024 (обс.) 12:30, 14 февраля 2018 (UTC)

А что тут не так? Продолжение вещественной нормы однозначно, если мы хотим продолжать вещественную норму, и продолжение p-адической нормы однозначно, если мы хотим продолжать p-адическую норму. Как говорили классики, «как пожелаем, так и сделаем». LGB (обс.) 12:47, 14 февраля 2018 (UTC)

Чтобы не возникло неоднозначности, должно быть задано, какая норма на R. Mx1024 (обс.) 13:22, 14 февраля 2018 (UTC)

В статье подробно и конструктивно описано понятие модуля комплексного числа и указано, что для вещественного подполя оно совпадает с абсолютной величиной. На мой взгляд, этого достаточно, я не вижу никаких причин отбивать хлеб у статей Норма (теория полей) и Норма (математика), для данной статьи это излишняя детализация. LGB (обс.) 13:53, 14 февраля 2018 (UTC)

«В статье подробно и конструктивно...» Напомню, тема обсуждения — раздел аксиоматики. Система аксиом должна быть такой, чтобы ею однозначно определялось, какая норма и топология поля C. Аналогично тому, как для действительных чисел (Энциклопедия элементарной математики, книга 1, стр.223-224) аксиомы XI, XII определяют топологию поля действительных чисел. Mx1024 (обс.) 14:59, 14 февраля 2018 (UTC)

Обратите внимание, «однозначно определяется», это вовсе не означает, что в аксиоме явно что-то говорится о топологии. Так же как в Энц. элем. матем. (стр.223-224) в самих аксиомах нет слов таких «топология», «норма» и т.д. Mx1024 (обс.) 15:36, 14 февраля 2018 (UTC)

Энциклопедия элементарной математики с вами не согласна, она содержит в точности ту же аксиоматику для комплексных чисел, что и наша статья. Можете найти источник, в котором аксиоматика такая же, но содержит дополнительные аксиомы? LGB (обс.) 15:41, 14 февраля 2018 (UTC)

LGB, Вам предупреждение ВП:НЕСЛЫШУ. «Можете найти источник» Источник я уже указал — Энциклопедия элементарной математики (ЭЭМ), книга 1, стр.223-224, стр.228. Так что можно исправить в соответствии с ЭЭМ. Mx1024 (обс.) 16:31, 14 февраля 2018 (UTC)

Что-то вы странное пишете. Стр. 223-224 в ЭЭМ — это аксиомы R, которые в разделе нашей аксиоматики и без того считаются выполненными. Стр. 228 содержит точно такую же аксиоматику, что и статья. Никаких дополнительных аксиом для комплексного поля ЭЭМ не предлагает. Возможно, вы имеете в виду, что надо сделать предварительную оговорку перед аксиоматикой, что упоминаемое в ней R понимается со всеми его классическими свойствами как нормированного и топологического пространства. Но в статье и так сказано, что «свойства R предполагаются известными». Чтобы нам закончить эту затянувшуюся дискуссию, предлагаю расширить данную фразу: «свойства R как поля, нормированного и топологического пространства предполагаются известными». Устраивает? LGB (обс.) 16:46, 14 февраля 2018 (UTC)

«Возможно, вы имеете в виду, что R понимается со всеми его классическими свойствами». Да, именно это я имею в виду. Mx1024 (обс.) 17:17, 14 февраля 2018 (UTC)

Сделал правку, чтобы ясно было видно, что я предлагаю. Другой вариант формулировки аксиомы C12 — указать здесь ссылку на аксиомы R

Аксиома C12. C содержит подполе, для которого выполняются аксиомы поля вещественных чисел.

Mx1024 (обс.) 17:43, 14 февраля 2018 (UTC)

Я убрал фразу «удовлетворяет приведенной аксиоматике», чтобы не было недоразумений, и заменил сноску на более ясную. В таком виде у меня замечаний нет. LGB (обс.) 18:31, 14 февраля 2018 (UTC)

Правки Zaur Ahmetov

Zaur Ahmetov произвёл в статье полную культурную революцию, произвольно переставив разделы. Подобные залихватские реновации, тем более в статье, претендующей на ИС, следует хотя бы предварительно обсудить, потому что порядок разделов был автором методически тщательно продуман в интересах читателя. В результате революции статья приобрела катастрофически нелепый вид с точки зрения методологии. После преамбулы идут формы представления, подразумевающие глубокое знакомство с комплексной арифметикой, и только затем (!!!) определяются операции с комплексными числами. Убедительно прошу уважать труд коллег и больше так не делать и не выставлять статьи Википедии на общее посмешище. Порядок я вернул. LGB (обс.) 11:31, 21 февраля 2018 (UTC)

Возражение

LGB Разделы переставлены не произвольно, а исходя из логики: вначале должно быть определение понятия, затем его представления и только потом действия с ним. А вовсе не наоборот, как у автора. И не понятно с какой точки зрения методологии "Геометрическое представление" например идёт отдельно от "Формы представления комплексного числа", а начинается всё сразу с Комплексной арифметики". Есть какое-то методологическое объяснение? Без подразумевания знакомства с арифметикой и комплексной в частности читать данную статью рановато. Хотя конечно обсудить надо, раз уж возникли разногласия, но без ругани и кавалерийских наскоков. Zaur Ahmetov (обс.) 12:10, 25 февраля 2018 (UTC)

Комплексная арифметика
1.1 Связанные определения
1.2 Сложение и вычитание
1.3 Умножение
1.4 Деление
1.5 Другие операции
1.6 Основные отличия комплексных чисел от вещественных
2 Геометрическое представление
2.1 Комплексная плоскость
2.2 Модуль
2.3 Аргумент
2.4 Сопряжённые числа
3 Формы представления комплексного числа
3.1 Алгебраическая форма
3.2 Тригонометрическая форма
3.3 Показательная форма

Вы написали, что «исходя из логики, вначале должно быть определение понятия, затем его представления и только потом действия с ним». Можете привести пример учебника, где придерживаются столь странной схемы? Передо мной школьные учебники; во всех сначала определяются арифметические действия, и лишь потом, скажем, тригонометрическая форма. В справочнике элементарной математики Выгодского то же самое. У вас же понятия модуля и аргумента в разделе «Тригонометрическая форма» употребляются до того, как они определены. Фраза «Арифметические операции для комплексных чисел имеют те же свойства» в вашей версии звучит загадочно, потому что никакие операции ещё не определены, они у вас определяются гораздо ниже, в 3-м разделе. Всё равно как в учебнике арифметики перечислять способы деления чисел и лишь затем определить, что такое деление. Геометрическое представление освещено раньше, чем прочие, по двум причинам: в силу его особой важности и в силу того, что оно ничем существенным не отличается от стандартного представления (парами чисел).

Основной принцип методологии: всё оформление статьи должно быть в интересах читателя. Я не завидую читателю, который впервые изучал бы материал по вашей версии статьи. Сожалею, если был слишком резок, но просто отменить ваши правки я не мог, вслед за ними была куча других, вполне доброкачественных, и мне пришлось битый час восстанавливать порядок вручную. LGB (обс.) 12:52, 25 февраля 2018 (UTC)

«Логические основания» или «Аксиоматика, модели и непротиворечивость»?

@Alexei Kopylov: предложил заменить название раздела «Логические основания» на «Аксиоматика, модели и непротиворечивость». Приглашаю сообщество высказать своё мнение, какой вариант лучше. LGB (обс.) 10:50, 25 февраля 2018 (UTC)

Различные модели аксиоматики

Те свойства модели аксиоматики, которые следуют из аксиом, являются одинаковыми для любых моделей. Для аксиоматики C1-C14, любые модели эквивалентны как поля. Эквивалентны как топологические пространства. Что касается поля p-адических чисел (и расширений этого поля), они не являются моделью приведенной в статье аксиоматики C1-C14. Mx1024 (обс.) 12:17, 4 мая 2018 (UTC)

Удалять из статьи текст, содержащий ссылку на АИ, можно только сославшись на другое АИ. Вашего личного мнения тут недостаточно. Фразу «As fields, C isomorphic to $Q_{p},$ but not as topological fields» я обнаружил сначала в английской версии статьи, затем проверил по источнику. Текст статьи с этой фразой см. тут, это Университет Нотр-Дам. Автор статьи, Andrei Jorza — assistant professor в этом университете, его компетентность неоспорима. Поэтому я не буду спорить по существу (норма в аксиомах 1-14 не участвует), а попрошу вас дать АИ с доказательством, что если структуры эквивалентны как поля, то непременно эквивалентны как топологические пространства. Пока восстановил спорный текст. LGB (обс.) 12:58, 4 мая 2018 (UTC)

@LGB:, Вы написали «норма в аксиомах 1-14 не участвует». Вы действительно не понимаете, как аксиомы 1-14 определяют норму и топологию? Предлагаю Вам разобраться с этим вопросом (как в аксиомах C1-C14 задается топология). Mx1024 (обс.) 13:51, 4 мая 2018 (UTC)

Я удалил текст, т.к. $Q_{p}$ не является моделью аксиоматики. И это соответствует АИ, который Вы привели: « C not isomorphic to $Q_{p},$ as topological fields».Mx1024 (обс.) 13:54, 4 мая 2018 (UTC)

Вы обходите полным молчанием приведенный мной АИ, подтверждающий обсуждаемую фразу, и пытаетесь обсудить спорный вопрос «по существу». Но мы с вами не общепризнанные эксперты и не имеем права подменять АИ своими личными мнениями. Если вы считаете, что Andrei Jorza ошибается, укажите АИ, который доказывает это. Если же он прав, то никаких оснований удалять обсуждаемый фрагмент нет.

Что-то мне подсказывает, что к консенсусу мы с вами не придём. Предлагаю, чтобы не спорить зря, вынести вопрос на форум проекта Математика или пригласить посредника. LGB (обс.) 15:24, 4 мая 2018 (UTC)

Вы пишете «обходите полным молчанием приведенный мной АИ», после моего ответа, где я ссылаюсь на этот АИ. «Алгебраическое замыкание поля p-адических чисел является моделью аксиоматики C1-C14.» Считаете Вы верным это утверждение? Mx1024 (обс.) 15:57, 4 мая 2018 (UTC)

Вы пишете: «приведенный мной АИ, подтверждающий обсуждаемую фразу». В приведенном АИ написано что-нибудь о том, является ли алгебраическое замыкание поля p-адических чисел моделью аксиоматики C1-C14 ? Mx1024 (обс.) 17:16, 4 мая 2018 (UTC)

[2] Не алгебраическое замыкание, а пополнение алгебраического замыкания поля p-адических чисел изоморфно C как полю. Mx1024 (обс.) 17:44, 4 мая 2018 (UTC)

Andrei Jorza пишет именно об алгебраическом замыкании ${\overline {Q}}_{p}$, а не о метрическом пополнении ${\overline {C}}_{p}$. LGB (обс.) 18:11, 4 мая 2018 (UTC)

Хорошо, сделаю ещё одну попытку достичь согласия.

1. Аксиомы 1-14 определяют поле комплексных чисел.
2. Согласно Нечаеву («Числовые системы», стр. 166), все поля комплексных чисел изоморфны как поля. И обратно, всякое поле, изоморфное C как поле, удовлетворяет аксиомам 1-14.
3. Согласно Andrei Jorza, «as fields, C isomorphic to ${\bar {Q}}_{p}$ but not as topological fields». Напомню, что ${\overline {Q}}_{p}$ у него обозначает алгебраическое замыкание $Q_{p}.$ Как я понял, вы эту фразу не отрицаете.

Но именно перевод этой фразы и стоит в статье. Если я вас не убедил, возобновляю предложение вынести тему на форум или пригласить посредника. LGB (обс.) 17:52, 4 мая 2018 (UTC)

«всякое поле, изоморфное C как поле, удовлетворяет аксиомам 1-14.» Неверно. Прошу подтвердить Ваше сообщения. Вы действительно считаете, «всякое поле, изоморфное C как поле, удовлетворяет аксиомам 1-14.» ? Если так, Вам следует ограничить доступ к этой статье. Mx1024 (обс.) 18:25, 4 мая 2018 (UTC)

Сейчас просмотрел текст Andrei Jorza. Откуда, где опубликован? Это вообще никакой не АИ. Mx1024 (обс.) 18:25, 4 мая 2018 (UTC)

Причина моих правок 04 мая 2018. «Алгебраическое замыкание поля p-адических чисел не является моделью аксиоматики C1-C14.» LGB в качестве аргумента приводит ошибочное утверждение «всякое поле, изоморфное C как поле, удовлетворяет аксиомам 1-14». Таким образом выводы LGB несостоятельны (т.к. основаны на ошибочном утверждении). Mx1024 (обс.) 05:32, 5 мая 2018 (UTC)

Вы грубо нарушили правило ВП:ВОЙ:

Если разногласия вызывает первая же версия новосозданной страницы, она не считается довоенной. Участники, имеющие претензии к содержимому такой страницы, вправе удалить из неё все спорные, по их мнению, фрагменты; версия после этого считается консенсусной и спорные правки в ней должны быть заранее обсуждены.

Вы так и не привели ни одного АИ в пользу своей точки зрения и проигнорировали мои предложения обсудить на форуме или пригласить посредника. Похоже, вам даже в голову не приходит, что вы можете ошибаться. Обращаю внимание на то, что данная избранная статья активно обсуждалась три месяца, и никто из участников-математиков не выдвинул возражений против данной фразы. Я вынужден восстановить консенсусную версию и обратиться к администрации, заодно вынесу проблему на форум. Пусвть сообщество решает, кто прав. LGB (обс.) 10:36, 5 мая 2018 (UTC)

• Комплексные числа и замыкание р-адических действительно изоморфны как поля, но не эквивалентны как топологические векторные пространства (если взять любой ненулевой элемент и его кратности, в комплексном случае получится дискретное множество, а в р-адическом - нет).
• Вопрос в том, считаем ли мы, что вещественные числа (и мнимая единица) выбраны внутри предполагаемых комплексных чисел? Если нет, то зачем мы их вообще упоминаем? Если да, то как мы их выбираем внутри замкнутых р-адических чисел? Видимо, неконструктивно, путём изоморфизма с комплексными, что бессмысленно.
• При этом фраза про то, что не все свойства моделей одинаковы, как будто важна, но ненышние аксиомы (которые просто запутанным способом говорят, что $\mathbb {C} =\mathbb {R} [i]$) для этого не подходят. Сама англовики использует описание "алгебраически замкнутое поля характеристики нуль с континуальным базисом трансцендентности", которое я предложил бы добавить.
• Есть модели в теории моделей в логике первого порядка, но там тупо существует счётная модель, то есть как поля они не обязательно изоморфны. Контекста, в котором и следует изоморфность полей, и можно употреблять слово "модель" я, увы, не знаю. Russian translator (обс.) 12:48, 5 мая 2018 (UTC)
  • Ничего не имею против предложенных вами дополнений и уточнений, вставьте, что считаете нужным. Хочу также заметить, что обсуждаемая фраза относится к любым построениям комплексных чисел, не обязательно к приведенным аксиомам C1-C14. В соседней фразе упоминается прямое построение C на основе ZFC, там могут быть свои тонкости. LGB (обс.) 18:44, 5 мая 2018 (UTC)

Аксиома C12 (содержит поле вещественных чисел)

Раздел «Аксиоматика комплексных чисел» статьи написан на основе 1) Нечаев В. И. Числовые системы. 2)Энциклопедия элементарной математики (в 5 томах). — 1951. — Т. 1.

В Энциклопедии элементарной математики написано.

(том 1, стр.223-224) Полем действительных чисел D называется непустое множество, в котором выполняются ... XI.Аксиома Архимеда. XII.Аксиома полноты. Условия I-XII означают, что D — непрерывное поле.

(том 1, стр.228) Определение 1. Поле комплексных чисел K называется минимальное поле, содержащее поле действительных чисел D, ...

Нечаев В. И. Числовые системы. В параграфе 8 Нечаев приводит аксиомы действительных чисел: 1) аксиомы операций поля, 2) аксиомы порядка, 3) аксиома полноты.

(Нечаев, стр.126) «системой действительных чисел называется линейно и архимедовски упорядоченное поле, всякая фундаментальная последовательность элементов которого сходится»

Еще один источник [3] Здесь вместо аксиомы "содержит R" явно перечислены аксиомы R. Среди аксиом есть аксиомы порядка и аксиома о существовании точной верхней грани.

Вывод. Согласно приведенным источникам, термины действительные числа, поле действительных чисел — это не просто поле. Они означают непрерывное поле, архимедово, линейно упорядоченное. Аксиома C12 означает, что C содержит R, как непрерывное линейно упорядоченное поле. Mx1024 (обс.) 12:45, 6 мая 2018 (UTC)

• Невозможно понять, что предлагается изменить и как это согласуется с целостными аксиомами. И да, посвежее 1951 года источник бы, там таких раритетных вещей понапишут. Russian translator (обс.) 17:07, 6 мая 2018 (UTC)

"посвежее 1951 года" И в 1951, и в 1851 было a+b = b+a. :) Вы считаете ЭЭМ не является АИ? Приведено 3 источника. Mx1024 (обс.) 17:46, 6 мая 2018 (UTC)

Так как на R определен линейный порядок, то для каждого x мы знаем, x>0 или x<0. Функция |x| определяет норму и топологию. Аксиоматика C1-C12 задает линейный порядок на R, который однозначно определяет норму и топологию. Mx1024 (обс.) 17:46, 6 мая 2018 (UTC)

Изоморфизм моделей аксиоматической теории

«Изоморфны как поля» — это не то же самое, что «модели изоморфны». Примеры. Имеется два расширения (C, R), (C',R').

• Пример 1. Изоморфизм полей f:C->C', который не переводит R в R'. Не является изоморфизмом расширений. Не является изоморфизмом моделей.
• Пример 2. Поля C и C' изоморфны. На R обычный линейный порядок. Порядок на R' не является линейным и не удовлетворяет аксиомам. Так что (C',R') не является моделью. Mx1024 (обс.) 09:12, 7 мая 2018 (UTC)
• Нужно вынести кусочек в другой раздел и немного переформулировать, поняли же уже двумя секциями выше, к чему относится фраза про разные свойства моделей. Сейчас мне неудобно, но к концу недели я постараюсь предложить исправленный вариант. Товарищ Mx1024, вместо войны правок можно поискать в источниках про альтернативные аксиомы. Russian translator (обс.) 13:40, 7 мая 2018 (UTC)

Можно уточнить

«C схоже с полем рациональных функций Q(xi)» — неопределённая формулировка, которую можно уточнить. Схоже чем? Много признаков, по которым поля могут быть похожими или отличаться. Mx1024 (обс.) 19:28, 7 июня 2018 (UTC)

• Коллега, с каждой Вашей правкой становится сложнее понять, о чём была речь изначально - вот в последней версии было написано так, как будто есть некий канонический изоморфизм, хотя он бывает только неконструктивный. Пожалуйста, если Вы недостаточно владеете темой, прекратите вносить исправления без обсуждения на СО. Викизавр (обс.) 18:23, 11 июня 2018 (UTC)
  • «написано так, как будто есть некий канонический изоморфизм» Wikisaurus, приведите точную цитату, о какой правке Вы говорите, которую «сложно понять», где говорится о «неком каноническом изоморфизме». Mx1024 (обс.) 18:57, 11 июня 2018 (UTC)
    • Эквивалентность норм подразумевает, что они заданы на одном пространстве или на двух разных, между которыми задан изоморфизм. Здесь никакого канонического изоморфизма нет, ну как между двумя векторными пространствами одной размерности. Смысл фразы в том, что при любом выборе не получится. Викизавр (обс.) 21:48, 11 июня 2018 (UTC)
      • Речь идет о нормах на одном пространстве, на ${\overline {\mathbb {Q} }}_{p}$. После того, как задан изоморфизм с C, на множестве ${\overline {\mathbb {Q} }}_{p}$ определена p-адическая норма и обычная норма C (которая, определяется изоморфизмом с C). Mx1024 (обс.) 09:15, 12 июня 2018 (UTC)

Правка 21:37, 11 июня 2018 [4] Комментарий: «такие нормы определены на различных пространствах, говорить об их эквивалентности нет смысла,» Wikisaurus, о каких нормах Вы написали в этом комментарии? Какие нормы, какие различные пространства? Mx1024 (обс.) 09:53, 12 июня 2018 (UTC)

@Wikisaurus: ответьте, пожалуйста на вопросы. Без ответа, Ваша правка рассматривается как вандализм и будет отменена. Mx1024 (обс.) 23:19, 12 июня 2018 (UTC)

• ВП:НЕВАНДАЛ, коллега. Подождите комментариев сторонних участников: ваши повторные внесения исправлений в статью нарушают ВП:ВОЙ. Викизавр (обс.) 23:31, 12 июня 2018 (UTC)

@Wikisaurus:

1. Был задан Вам вопрос о Вашем комментарии к правке. Вы ничего не ответили.
2. Приведен ответ на Ваше замечание (см. выше текст «Речь идет о нормах на одном пространстве,...» ). Вы ничего не ответили, означает Вам нечего сказать, аргументов нет. В связи с отсутствием ответа Ваша правка отменяется. Mx1024 (обс.) 23:52, 12 июня 2018 (UTC)

Mx1024 и авторитетность источников

Mx1024 добавил в двух местах статьи шаблон «Проверить авторитетность». Согласно документации к шаблону:

Шаблон используется для пометки данных, предположительно основанных на неавторитетном источнике. Добавляйте этот шаблон только после того, как вы проверили авторитетность источника.

Таким образом, как и полагается повсеместно, бремя доказательства неавторитетности лежит на том, кто в ней усомнился. Mx1024 нарушил руководство, причём, что особенно огорчительно, необоснованно испортил избранную статью. Речь идёт о сайтах:

1. Калифорнийский университет, Беркли, см. Вики-статью о нём, это государственный исследовательский университет США. Автор статьи, Christopher Eur, пишет о себе: «I completed my undergraduate studies at Harvard University in mathematics», сейчас дополнительно заканчивает университет в Беркли. Специализируется по коммутативной алгебре и алгебраической геометрии.
2. Университет Нотр-Дам, см. Вики-статью о нём, это католический частный элитный университет, основан в 1842 году. Автор статьи, указанной в сноске — Andrei Jorza — assistant professor в этом университете.

Как видите, это не шарашкины конторы и вполне компетентные специалисты. Либо строго докажите, что сноски ведут на неавторитетный источник, либо выходите на ВП:КОИ для общего обсуждения. Я уж не говорю о том, что вы дважды признали — цитированную в нижней сноске фразу вы полностью принимаете. До окончания обсуждению удалю произвольно выставленные шаблоны. LGB (обс.) 16:20, 11 июня 2018 (UTC)

Я согласен, «неавторитетность» неподходящий шаблон, т.к. к самим данным у меня замечаний нет. Смысл моей правки — в указании более подходящего источника. Аспирант [5] это еще не значит компетентный специалист.

• АИ доцента [6] будет статья, опубликованная в научном журнале, а не текст в Интернете.
• Для русскоязычного читателя более предпочтителен источник на русском языке.
  LGB, укажите, пожалуйста ссылки на страницы которые содержат информацию и ссылки на рассматриваемые pdf-файлы. Например, на странице [7] ссылка «notes for Math 162b, Caltech, Winter 2012» указывает на другой pdf-файл.
  Mx1024 (обс.) 18:16, 11 июня 2018 (UTC)

Просьба не удалять шаблоны до окончания обсуждения. Mx1024 (обс.) 21:29, 11 июня 2018 (UTC)

Согласно правилу ВП:АИ, наличие печатного издания не является обязательным условием для признания авторитетности источника. Цитирую:

С бо́льшим доверием следует относиться к книгам, опубликованным:

• издательствами крупных вузов (Издательство Оксфордского университета, Издательство Кембриджского университета, Издательство МГУ и т. д.), научно-исследовательских институтов, национальных академий наук (Издательство «Наука», National Academies Press);
• ведущими мировыми издательствами научной литературы (Springer, Wiley, Academic Press и т. д.);
• авторами, являющимися уважаемыми экспертами в данной области<...>

Полнотекстовые онлайновые источники так же приемлемы, как и офлайновые, если они такого же качества и надёжности. Читатели могут предпочитать онлайновые источники, поскольку они легко доступны.

Сейчас многие уважаемые авторы публикуют свои статьи на интернет-сайтах, и никто не ставит им это в вину. Например, очень добротная статья по p-адической теории вообще и топологии в частности есть у Andrew Baker: An Introduction to p-adic Numbers and p-adic Analysis, там аналогичные идеи. Бейкер — это Университет Глазго, Шотландия, см. тут. Если это вас устроит, могу сослаться на него вместо обсуждаемых сносок.

Ваше замечание «Аспирант это еще не значит компетентный специалист» теоретически допустимо, если у вас имеются конкретные основания для такого сомнения. Если таких оснований нет, разумно выйти на форум ВП:КОИ для детального обсуждения. Ставить под сомнение сноску, содержание которой вы считаете вполне верным, только по причине отсутствия вашего личного доверия к автору — довольно странная позиция.

Запрос в последнем абзаце я не понял. В обеих сносках указаны точные URL.

И последнее. Вам уже дважды приводили правило, согласно которому в случае разногласий статья фиксируется в довоенном уровне до конца обсуждения. Я восстанавливаю довоенный текст, убедительно призываю вас не затевать новую войну правок. LGB (обс.) 17:55, 12 июня 2018 (UTC)

1. ВП:НЕСЛЫШУ «С бо́льшим доверием следует относиться к книгам,», «Полнотекстовые онлайновые... если они такого же качества и надёжности» Речь идёт не о книгах и не об источниках «такого же качества».
2. ВП:НЕСЛЫШУ «статья есть у Andrew Baker», речь идет не о статье Andrew Baker
3. ВП:НЕСЛЫШУ «отсутствия вашего личного доверия к автору», это не мое личное, а правила ВП:АИ
4. ВП:НЕСЛЫШУ «В обеих сносках указаны точные URL.» Где в Интернете на страницах авторов указаны ссылки на эти pdf-файлы? На личной странице Andrei Jorza нет такого файла. Он заменил его на новую версию.
5. ВП:НЕСЛЫШУ «» Более предпочтителен источник на русском языке. Mx1024 (обс.) 19:35, 12 июня 2018 (UTC)

Так как у Вас никаких аргументов нет, восстановите, пожалуйста, шаблон. Mx1024 (обс.) 19:35, 12 июня 2018 (UTC)

• Пока еще сообщество не приняло правило об оценке источников по этой таблице, придется разбираться по существу :).
  Итак, первый источник - текст непонятного статуса. Автор - его студент (в то время еще даже не аспирант). Текст не опубликован даже в виде препринта. Статус текста не ясен, что это конспект лекций или что-то еще? Нужно найти более авторитетную замену. Второй источник - текст с описанием университетского курса, составленного профессором. Лекции специалиста в профильных университетах (а значит и сопутствующие материалы) могут быть источниками для информации, по крайне мере, когда она не вызывает споров. Однако подобного типа материалы зачастую могут содержать ошибки. Желательно найти учебник или рецензируемую статью - такие тексты более тщательно проверяются.
  Кроме того, Mx1024 прав: из голой ссылки на pdf файл неясен статус этих файлов. Если автор не дает ссылку на свой файл ни на странице курса, ни на своей домашней странице, то вряд ли этот файл можно считать опубликованным. Откуда мы знаем что это за файл? Может это черновик, который автор держит для себя, и о существовании, которого давно забыл.
  — Алексей Копылов 07:28, 13 июня 2018 (UTC)
  • Спасибо за вашу правку, она помогла мне отыскать и вставить суперавторитетный источник, который, как я надеюсь, завершит эту затянувшийся спор. Спорные сноски я удалил. LGB (обс.) 16:17, 13 июня 2018 (UTC)

Соответствие норм

Правка 18:10, 11 июня 2018. Комментарий: «есть смысловая разница между "неэквивалентны" и "не могут соответствовать при любом отождествлении", потому что такие отождествления неконструктивны» Неясно, что имел в виду участник. Неконструктивность никакого значения не имеет. p-адическая норма не может соответствовать обычной норме — как раз является следствием неэквивалентности. Mx1024 (обс.) 21:26, 11 июня 2018 (UTC)

TODO

Сопряжённые числа

Раздел Сопряжённые числа помещен после Деления, а при определении деления сопряжённые числа вообще не упоминаются. Уже в самом начале статьи можно поместить краткое определение. Mx1024 (обс.) 21:50, 12 июня 2018 (UTC)

Стилевые правки

• «можно сравнивать на равно/не равно»
• «то есть избавиться от мнимости в знаменателе», «избавиться от мнимости».
• «$\varphi$ определяется с точностью до целого кратного $2\pi$.»

Mx1024 (обс.) 21:55, 12 июня 2018 (UTC)

Расширение или Дополнение

Подзабыл я высшую математику, но не ошибка ли случаем: В шапке "Множество комплексных чисел обычно обозначается символом {\displaystyle \mathbb {C} ,} {\displaystyle \mathbb {C} ,} оно содержит множество вещественных чисел {\displaystyle \mathbb {R} } \mathbb {R} и может рассматриваться как его расширение." Расширение или Дополнение (Разность_множеств#Дополнение_множества)? lEdwardElric (обс.) 17:03, 12 августа 2018 (UTC)

Расширение поля — это строго определённый алгебраический термин, не имеющий прямого отношения к операциям разности множеств или дополнения подмножества. Почитайте. Поскольку преамбула рассчитана на школьников, то термин расширение там не разъясняется, так что можно понимать его в нестрогом смысле, просто как увеличение числа элементов. LGB (обс.) 17:08, 12 августа 2018 (UTC)

Произношение и ударение

Очень странное заявление, что в контексте чисел ударение на "о" допустимо. Указаны ссылки только на общие энциклопедии, что не отражают специфики математического языка. Ссылка на словарь Лопатина, вообще странная. Там нет контекста именно "чисел". Там указано, что в математике ударение может быть на "е", но нигде в нем не указано, что в этой же математике допустимо ударение на "о". В Большой Российской энциклопедии указано также ударение на "е" в данном контексте. Если взять, например Математический энциклопедический словарь./Гл. ред. Ю. В. Прохоров.— М.: Сов. энциклопедия, 1988.— 847 с. То в нем четко указано, что ударения в словах имеющих отношения к теме комплексных чисел, имеют ударение на "е". В другом же контексте слово имеет ударение на "о". Специалисты так же в основном указывают на вариант с ударением на "е".

Предлагаю добавить ссылок на словари не общего содержания, а математического. Кроме того, по-моему следует указать, что в данном контексте все же более распространено ударение на "е", хотя на "о" иногда рассматривается как допустимое. — Эта реплика добавлена участником OdiEtProieci (о • в)

Этот вопрос уже подробно обсуждался, см. Обсуждение:Комплексный анализ#Ударение в слове «Комплексный» в Москве. Обоснование двойного ударения в статье подробное и максимально авторитетное. Двойное ударение ставили в БСЭ 2-го издания, в статье КОМПЛЕКСНЫЕ ЧИСЛА, которую писали профессиональные математики — они, по-вашему, «не отражают специфики математического языка»? В БРЭ 3-го издания есть статья КО́МПЛЕКСНЫЙ АНАЛИЗ — её тоже писали не знающие специфики? В словаре Лопатина сказано: ко́мплексный и компле́ксный (матем.); вы пишете: нигде в нем не указано, что в этой же математике допустимо ударение на О — очень причудливое и ни на чём не основанное истолкование вполне ясной фразы Лопатина о том, что общенормативное ударение на О, но в математике встречается и ударение на Е. У шахтёров и моряков тоже встречаются варианты дОбыча и компАс, но разве кто-нибудь запрещает им использовать общенормативные ударения? Указанное вами особое мнение Математического энциклопедического словаря никак не перевешивает преобладающего мнения профессиональных математиков и языковедов, источники приведены в статье. Ваши фразы «Специалисты в основном указывают на вариант с ударением на Е» и предложение считать ударение на Е более распространённым не подкреплены никакими ссылками на сравнительные исследования, а личные мнения в Википедии запрещены. LGB (обс.) 14:03, 20 июня 2019 (UTC)

Во первых почему БСЭ авторитетный источник?, это просто общая энциклопедия, не надо ее возводить в ранг источника уровня терминологии для математики. Кроме того БСЭ уже устарела. Вы упоминаете БРЭ и при этом совершенно упускаете факт, что в БРЭ в слове комплексные числа ударение указано, как раз вполне на "е". А БРЭ более современный источник чем БСЭ. Вариант с кОмплексным анализом вообще есть только там, и он наоборот выглядит весьма странно. Если уж числа комплЕксные, то анализ должен быть комплЕксным. Но это не суть. Лопатинский словарь никоем образом не дает понять допустимо ли в математике, в контексте чисел говорить с ударением на "о". Вывод который вы делаете тоже возможен, но вообще говоря не обязателен. Аргумент с компАсом странен. Компас - не терминология, это профессиональный жаргон. Все-таки между терминологией научного сообщества и жаргоном есть различия. Какого преобладающего мнения специалистов и языковедов? Вы мне говорите про то, что я ни на что не ссылаюсь (хоть я и ссылаюсь) и просто высказываю личное мнение. Но вы то ссылаетесь по сути на один источник и говорите что это преобладающее мнение. Над чем? БРЭ и указанный мною источник говорят что ударение на Е. И совершенно неважно кто там писал БСЭ, БСЭ - как и ВСЕ источники указанные в статье - это источники рассчитанные на непрофессионалов. Еще большинство и довольно старые. Но у меня лишь один вопрос, почему не указано совершенно специализированных источников? По-моему такое цитирование несколько однобокое. Все о чем я по сути говорю, это указать еще источники, специализированного назначения, чтобы у читателя была более полная картина. OdiEtProieci (обс.) 10:36, 22 июня 2019 (UTC)

Что-то неважно у вас с аргументацией, а также с объективностью.

БСЭ уже устарела. И это говорит человек, единственный АИ которого (Математический энциклопедический словарь) датируется 1988 годом.

Вы совершенно упускаете факт, что в БРЭ в слове комплексные числа ударение указано, как раз вполне на "е". А вы совершенно упускаете факт, что в БРЭ в статье КОМПЛЕКСНЫЙ АНАЛИЗ ударение указано, как раз вполне на "О". Разумеется, это разногласие говорит о паршивом уровне редактирования БРЭ — добросовестный редактор заметил бы этот ляп и поставил двойное ударение, как в БСЭ, в обоих случаях, — однако само существование этого ляпа неопровержимо свидетельствует, что ваше утверждение о доминировании ударения на Е ошибочно.

Ударение «комплЕксный» — такой же профессиональный жаргон, как и дОбыча с компАсом, какая разница, в какой среде жаргон — в рабочей или научной? У юристов, даже учёных, свой жаргон, они говорят: осУжден. Ну и что, будем им запрещать общенормативный вариант «осуждЁн»?

Что-то наша дискуссия пошла ВП:ПОКРУГУ. Вы утверждаете, что надо добавить источники. Какие? Источники, в которых говорится, что ударение на Е грамотно, а на О неграмотно? Таких не существует. Все приведенные в статье пять источников по правилам Википедии считаются высокодостоверными АИ, и они рекомендуют двойное ударение. Наличие особого мнения Матсловаря 1988 года общую картину не меняет, вопрос ударения решают не математики, а языковеды, а они ничего не имеют против общенормативного ударения на О. Давайте на этом закруглимся и не будем навязывать общественности свои личные предпочтения. LGB (обс.) 11:12, 24 июня 2019 (UTC)

• Вы отметаете Матсловарь как непрофильный, но при этом считаете мнение БРЭ, где, судя по всему, вообще нету редактуры, не то что лингвистической? Викизавр (обс.) 11:52, 24 июня 2019 (UTC)

Единственное, что я хочу доказать — это что существуют два одинаково уважаемых варианта (both alike in dignity, © Shakespear), и нет оснований произвольно отметать один из них. LGB (обс.) 12:02, 24 июня 2019 (UTC)

• Нет, вариант с ударение на о существует только где-то на Самарском мехмате и в словарях, а указывать маргинальный вариант как равноправный — грубое нарушение ВП:ВЕС. Викизавр (обс.) 12:14, 24 июня 2019 (UTC)

Если вы найдёте авторитетное подтверждение мнению о маргинальности ударения кОмплексный, оно будет немедленно отражено в статье. LGB (обс.) 12:19, 24 июня 2019 (UTC)

• Если из источников есть такая возможность, я бы выделили вариант компле́ксный как основной, всё-таки IRL только так и говорят. Викизавр (обс.) 10:21, 20 июня 2019 (UTC)

Бытует мнение, что петербургская школа предпочитает ударение комплЕксный, а московская — кОмплексный. Но я нигде не встречал авторитетные сравнительные исследования частоты употребления ударения в разных регионах России, а вы? LGB (обс.) 14:06, 20 июня 2019 (UTC)

• Очевидно, нет. Почитал обсуждение выше и понял так, что вы готовы биться за вариант на о до конца, так что я пас, но всё же спрошу из интереса - судя по ЛС, вы сами из Москвы; вы имеете какой-то контакт с московскими математиками? Вы хоть раз слышали, чтобы они ставили ударение на о? Я вот никогда не слышал, ни от студентов, ни от 70-летних дедушек, ни от олимпиадников, ни от прикладников, ни от чистых математиков. Викизавр (обс.) 00:01, 21 июня 2019 (UTC)

Ну, двойное ударение в приведенных АИ ведь откуда-то возникло, не масоны же его выдумали. Лично мне совершенно до лампочки, где мои собеседники ставят ударение в слове КОМПЛЕКСНЫЙ, хоть на Ы, это дело их вкуса. Разжигать новые священные войны остроконечников с тупоконечниками, мягко выражаясь, глупо. Моя цель — не агитировать за ударение на О, а призвать к терпимости и признанию права на собственное мнение, тем более что оно подтверждается рядом АИ. Обратите внимание — несмотря на обилие источников за двойное ударение, никто — подчёркиваю, НИКТО из сторонников ударения на О никогда не требовал срочного перехода всех на его сторону. Агрессивную нетерпимость проявляют исключительно сторонники ударения на Е, а это, как говорит общая социология, характерно для меньшинства, а не для большинства. Большинство, как правило, гораздо толерантнее. Что касается меня, то я учился на саратовском мехмате, там доминирует (эвакуированная в 1941 году) московская школа, и ударения были самые разные. О московском мехмате судить не рискну, если кто знает, пусть выскажется. LGB (обс.) 11:06, 21 июня 2019 (UTC)

В Москве тоже и так, и так говорят. Вот лекция Спивака, [8], ударение на первый слог, кОмплексные числа. --Fedor Babkin ^talk 12:24, 24 июня 2019 (UTC)

Да, верно. Вот ещё пример с ударением на О: Видеоуроки Владимира Романова: решение примеров. Правда, из какого он города, неясно. LGB (обс.) 12:52, 24 июня 2019 (UTC)

• Это не так. Я учился в московском вузе, а потом работал в поволжском вузе, и в обоих только говорили только "комплЕксные числа". Вообще откуда взялся этот бред, что кто-то говорит кОмплексные числа, непонятно. 216.154.8.52 05:35, 14 января 2023 (UTC)

Это заимствованное слово. В английском ударение на второй слог если это прилагательное, и на первый для существительного. Alexander Mayorov (обс.) 05:42, 21 июня 2019 (UTC)

• Английский тут не аргумент. В английском языке не используется способ различения разных значений слов путем ударения. 216.154.8.52 05:39, 14 января 2023 (UTC)
• Английский не аргумент. Во-первых, с чего вы взяли, что это слово заимствовано из английского, а не из французского или латинского? Во-вторых, в английском языке для ударений вообще нет никаких правил, они совершенно произвольные. Есть такие слова, о которых вы говорите, но к данному случаю это не имеет никакого отношения. В английском и "комплекс" и "комплексный" произносятся кому как нравится, с ударением и на первом, и на втором слоге, и даже с первичным ударением на один слог, но со вторичным на другой (т.к. в английском часто бывает два ударения, одно первичное, другое вторичное). И в словарях это отражено, например, в словаре Вебстера. 216.154.8.52 05:48, 14 января 2023 (UTC)

В статье на данный момент указано: "от лат. complex" (без указания источника), но в этимологических словарях (в том числе ru и en) указывается только форма лат. complexus – полагаю, следует уточнить форму (и, по возможности, сослаться на АИ) — lozovsky (обс.) 17:39, 25 июля 2021 (UTC)

Сделано. Leonid G. Bunich / обс. 18:29, 25 июля 2021 (UTC)

"Комплексные числа -- числа вида a + b*i" -- логическая бессмыслица.

"Ко́мпле́ксные чи́сла ... — числа вида a+bi, где a,b — вещественные числа, i — мнимая единица, то есть число, для которого выполняется равенство: i^2=-1." по своему месту в начале статьи воспринимается как основное определение, а фактически является полной ахинеей:

1) "мнимая единица, то есть число ..." -- какое такое число? Если вещественное, то таких не существует, если комплексное, то налицо порочный круг.

2) Даже если ввести комплексные числа другим путем, то у этого уравнения ( i^2=-1 ) два корня: какой выбираем для обозначения i? Если в одном месте выбрать (0,1), а в другом -- (0,-1), то легко получить цирк в духе 1=0.

3) a+bi -- это что? По обозначениям тут умножение и сложение с участием доселе неизвестной твари i. Как это делать? Сначала нужно определить операции с новыми числами, а потом уже писать выражения.

И всё это не формальные придирки. Такое "определение" ничуть не проясняет, что такое комплексные числа для человека, совершенно незнакомого с предметом, и не позволяет вывести практически никаких свойств этих чисел.

Это примерно эквивалентно тому, что написать: "Производная функции y=f(x)-- это функция вида y'=dy/dx, где dx -- дифференциал независимой переменной, равный ее приращению, а dy -- дифференциал зависимой переменной, т. е. величина, для которой выполняется равенство dy=y'*dx ".

При этом существует разумный, не слишком сложный, вполне понятный даже школьнику, но в то же время достаточно строгий способ введения комплексных -- в виде упорядоченных пар действительных (a,b) с добавлением правил для сложения и умножения.

88.147.152.113 17:18, 28 февраля 2021 (UTC)

Определение, которое вы лихо назвали полной ахинеей, взято из «Математической энциклопедии». Точно так же определяются комплексные числа в большинстве авторитетных источников (АИ), включая «Справочник по элементарной математике» Выгодского, Большую российскую энциклопедию и даже «Энциклопедический словарь юного математика». Ваши возражения не выдерживают критики.

1. Число $i$ вводится не как вещественное и не как комплексное, а просто как математический объект, свойство которого заданы аксиомой: $i^{2}=-1.$ Далее в данной статье доказывается непротиворечивость этой аксиомы другим и строится поле комплексных чисел. При этом $a+bi$ вначале определяется как формальная сумма, а далее доказывается, что её можно рассматривать как результат операции. Ваше возражение: «"мнимая единица, то есть число ..." -- какое такое число? Если вещественное, то таких не существует, если комплексное, то налицо порочный круг» с таким же основанием можно выдвинуть, например, на расширение натуральных чисел нулём: «"ноль, то есть число ..." -- какое такое число? Если натуральное, то таких не существует, если целое, то налицо порочный круг».
2. Точно так же число $i$ не определяется как квадратный корень или корень уравнения $x^{2}+1=0$.

Предложенное вами определение через пары (это подход Уильяма Гамильтона, 1837 год) нисколько не более строгое и даже не более понятное новичкам, поскольку требует изначально введения довольно странных и на первый взгляд совершенно искусственных правил для умножения пар. Подход из АИ гораздо более прозрачен. В данной статье гамильтонова модель используется для доказательства непротиворечивости аксиом комплексных чисел, где для неё самое подходящее место. Leonid G. Bunich / обс. 18:34, 28 февраля 2021 (UTC)

Если это аксиоматический подход, то тогда надо явно писать, что i^2=-1 это аксиома, а не определение. Ближе к концу этот подход изложен. Данная аксиома идет под номером С13, и не зря -- сначала нужно постулировать свойства сложения и умножения. Как видите, получается посложнее, чем с упорядоченными парами. А выхватывание двух свойств комплексных (i^2=-1 и z=a+bi) и создание из них "определения" -- это действительно ахинея, я привел пример с производной, там каждая формула тоже сомнению не подлежит, но "определение" бессмысленное.

Что же касается АИ, то нужно их больше привлечь и рассортировать по уровню авторитетности, например: 1) Учебники/справочники для математических факультетов, 2) Для технических факультетов, 3) для школ, тогда видно будет, что "побеждает", хотя такие вещи решать голосованием странно. Среди приведенных Вами источников два уже по названию -- в 3 категории. 88.147.152.113 11:09, 3 марта 2021 (UTC)

Все определения новых математических объектов опираются, в той или иной форме, на аксиомы, перечисляющие их свойства, почитайте Математический объект. Точно так же при расширении натуральных чисел определяются ноль и отрицательные числа, а именно аксиомами:

$0+a=a+0=a;\quad -a+a=0$

Теперь касательно АИ. Наиболее авторитетные АИ, то есть энциклопедии (первый класс, по вашей систематике), все до единой определяют комплексные числа так же, как и Википедия:

Большая российская энциклопедия

Большая советская энциклопедия, изд. 2 и 3 (первое не проверял)

Советский энциклопедический словарь

Математическая энциклопедия

Математический энциклопедический словарь

Кроме того, такое же определение содержат оба справочника Выгодского (по высшей и по элементарной математике), справочники Бронштейна и Семендяева, Корна и т. д. За рубежом положение аналогичное, см., например, книгу филдсовского лауреата Ларса Альфорса «Complex analysis». Кстати, почти все языковые разделы Википедии (кроме украинского) едины в таком определении комплексных чисел, а там тоже не дураки сидят, ахинею не пропустят.

Учебники, которые вы отнесли ко второму и третьему классу, в большинстве (по моим оценкам, 80%) также используют энциклопедическое определение, хотя я нашёл парочку сторонников вашего подхода (Евграфов и Привалов). Характерно, что для них первое издание опубликовано достаточно давно. Послеперестроечные издания подход через пары не упоминают, кроме переиздания старых учебников. Поэтому, в соответствии с правилами ВП:АИ, ВП:ВЕС и ВП:МАРГ, в качестве определения комплексных чисел однозначно было выбрано то, что в других энциклопедиях. Тем более что оно не хуже, а лучше гамильтоновского, как я уже пояснял. Leonid G. Bunich / обс. 15:53, 5 марта 2021 (UTC)

Я изучал высшую математику в Белорусском политехническом институте в 80-х годах. Преподаватель Соколова Нинель Мефодьевна давала понятие комплексного числа (КЧ) как упорядоченную пару $(a,b)$. Благодаря этому я не зацикливаюсь на мнимых числах, а рассматриваю их лишь как частный случай КЧ. Такой подход к изучению этого понятия не только делает его естественным, но и сразу внедряет в сознание идею развития понятия, например упорядоченной тройки $(a,b,c)$ и далее - матрицы, а дальше - насколько хватает воображения вплоть до многочисленных измерений пространства нашего обитания. Впоследствии я приобрел учебник Гусака Высшая математика (в 2-х томах) (кафедра ВМ Белорусского государственного университета), в котором ВМ излагается в том же порядке, в частности КЧ. Ударение комплЕксные считаю жаргоном в научной среде, а свое мнение подкрепляю логикой: пара $(a,b)$ это кОмплекс двух чисел, а не комплЕкс. Начиная изучение с непонятно откуда берущегося $i^{2}=-1$, вполне естественно впасть в этот жаргон. Очень жаль, что упорядоченная пара $(a,b)$ не попала в статье в перечень основных форм записи КЧ. Я бы вообще предложил считать ее единственной основной формой, а остальные - частными. Но конечно я понимаю, что множество математиков изучало КЧ, начиная именно с формулы $i^{2}=-1$, что произвело на них неизгладимое впечатление, и они до сих пор считают, что мнимая единица это то, ради чего придуманы эти числа, а ударение никак не связывают с понятием комплекса чисел. Я считаю это заблуждением. — Головорушко Сергей Яковлевич (обс.) 20:55, 2 апреля 2021 (UTC)
Хотел бы добавить еще свое мнение по геометрическому представлению КЧ. Считаю неправильным представление КЧ в виде точки на плоскости. Как и считаю неправильным представление обычных чисел (рациональных и действительных) точками на числовой прямой. На числовой прямой числа представляются отрезками, иначе - как их сравнивать? А точки это всего лишь концы отрезков, около которых ставят обозначение числа, хотя правильнее было бы ставить обозначения чисел около середин отрезков - просто это неудобно. С числами на комплексной плоскости сложнее - это не точки, не векторы и не отрезки. Это комплекс двух отрезков, расположенных на ортогональных координатных осях. Точка на плоскости позволяет найти концы этих отрезков по ее проекциям. С этой точки зрения она очень удобный инструмент для работы с КЧ. Поскольку оси координат это разные измерения (геометрические координаты это лишь частный случай), например - температура и длина, то сравнить их невозможно. Сравниваются только компоненты КЧ, находящиеся на одной оси. Собственно в строгом смысле и плоскости никакой нет, только оси. Плоскость лишь инструмент, как и точка на ней. Плоскость воображаемая, точка воображаемая, а отрезки на осях реальные. Мнимая единица очень удачный термин - она существует тоже только как инструмент, ни на плоскости, ни на осях ее нет. — Головорушко Сергей Яковлевич (обс.) 22:00, 2 апреля 2021 (UTC)

Вы имеете полное право на личное мнение по любому вопросу, включая способ определения комплексных чисел. Причины, по которым это мнение не может быть отражено в энциклопедии, подробно изложены выше. Leonid G. Bunich / обс. 08:07, 3 апреля 2021 (UTC)

Я не понял, к чему эта ваша реплика. Я не обращался к вам с просьбой отразить мое мнение в Википедии. А ответ в стиле "Останемся каждый при своем мнении" в математике допустим был в докомпьютерную эру и разве что в тех случаях, когда спать пора, а выяснение истины откладывается на завтра. Я может быть слишком деликатно выразился, не так, как 88.147.152.113, который числа вида $a+bi$ назвал логической бессмыслицей, и вы посчитали необязательным отвечать по существу. Но, упростив мои реплики, можно свести их к фразе "Автор статьи не понимает, что такое комплексные числа". Вы их не упростили и, видимо поэтому не поняли, о чем я говорю. Почему я так считаю? Я сейчас объясню.

КЧ не понимали те, кто учил автора, кто учил вас и кто учил ваших учителей (пожалуйста, не принимайте как оскорбление). Как не понимают гаджетов дети, но уверенно ими пользуются. Процесс понимания КЧ в среде математиков еще далеко не закончился. Что такое КЧ, я думаю, не понимал даже Гамильтон, который предложил упорядоченную пару. То понимание, которое предлагает автор статьи, это понимание, как пользоваться гаджетом, то бишь - использовать КЧ в вычислениях. Это связано с пониманием проблем, решаемых с помощью разных форм записи КЧ, но никак не с пониманием самого КЧ. Еще раз повторю: простейшее КЧ это упорядоченная пара действительных чисел. Это никак не мнимая единица. А в общем виде КЧ это число вида $(a,b,...,n)$, где $a,b,...,n$ - любые математические объекты, кроме, может быть, отношений. КЧ имел в виду Аристотель, когда говорил "Всё есть число". Главное свойство КЧ это далеко не $i^{2}=-1$. Главное свойство КЧ это ортогональность всех упорядоченных объектов. — Головорушко Сергей Яковлевич (обс.) 22:36, 3 апреля 2021 (UTC)

Уважаемый коллега, рекомендую вам ознакомиться с правилами ВП:АИ, ВП:ВЕС и ВП:МАРГ. Согласно этим правилам, в научных спорах Википедия обязана излагать сложившийся научный консенсус. Другими словами, в случае спора прав тот, кто сможет привести в подтверждение своей позиции больше авторитетных источников. При этом неважно, насколько непоколебимо его оппонент уверен в своей правоте, и даже неважно, какие несокрушимые доводы он приводит в пользу своей личной позиции. Предложенное вами «выяснение истины» также не является задачей Википедии. Если вас волнует именно это, рекомендую выйти на форум dxdy.ru, там очень компетентные ребята.

Определение комплексного числа в данной статье опирается (см. выше) на пять энциклопедий и четыре справочника. Чтобы продолжить наш спор, вы должны привести с десяток АИ того же уровня, подтверждающих вашу позицию. Простые рассуждения без источников нарушают правило ВП:НЕФОРУМ. Leonid G. Bunich / обс. 09:16, 4 апреля 2021 (UTC).

Не хочется мне продолжать то, что вы называете спором. Потому что, во-первых, думаю, что вы гораздо образованнее меня в математике, а во-вторых, я спором называю не голосование (кто больше АИ приведет), а только логическую аргументацию. А поскольку вы считаете, что "неважно, какие несокрушимые доводы он (оппонент) приводит в пользу своей личной позиции", то и не вижу в этом смысла. Останемся, как вы говорите, каждый при своем. На всякий случай приведу свой АИ, упомянутый выше. Я запамятовал фамилию автора, поэтому сделал тогда ошибку в его фамилии, за что приношу свои извинения. На самом деле АИ: А.А.Гусак. Высшая математика. Учебник для студентов вузов. Минск: ТетраСистемс, 2003. http://elib.bsu.by/handle/123456789/94419. Да, я не совсем понимаю, почему вы думаете, что я хочу непременно внести какую-то правку в статью о КЧ. Вовсе нет. Я полагаю, что эта секция, называемая "Обсуждение", предназначена для публикации мнений, которые могут повлиять на понимание тех или иных вопросов, в том числе и на изложение их автором статьи. Согласитесь, утверждение "Комплексные числа -- числа вида $a+b*i$, где $i$ - комплексное число, -- логическая бессмыслица" пока никак не опровергнуто. Как не опровергнуто утверждение "Числа на числовой оси изображаются отрезками, имеющими величину (длину), а не безразмерными точками". Я полагаю, такие претензии статья должна устранять, или хотя бы упомянуть о них. Замалчивание проблем их не устраняет. — Головорушко Сергей Яковлевич (обс.) 19:27, 4 апреля 2021 (UTC)

Правки Mylique

Участница Mylique сделала обширную правку, часть которой была отменена участником Alexei Kopylov. У меня есть дополнительные замечания (мелкие корректировки стиля не в счёт). Раздел «Связанные определения»

1. В определении комплексного числа $z=a+bi$ сказано, что $a,b$ вещественны. Зачем оговаривать этот факт повторно?
2. Как я уже вам писал, использование термина мнимое число неоднозначно и не рекомендуется. Вставил в статью небольшое разъяснение по этому поводу и убрал отовсюду сомнительный термин.

Раздел «Основные отличия комплексных чисел от вещественных»

1. Убрал излишне хитроумное выражение: «то количество корней (вообще говоря, комплексных), какому равна его степень».

Раздел «Замечания»

1. Фразу о сохранении алгебраических свойств при сопряжении я перенёс в более подходящее место. Никак не разъяснённое упоминание «двойственности» убрал.

Раздел «Комплексная плоскость»

1. Фразу об обосновании убрал. В энциклопедии не требуется обоснование, этим занимаются АИ, на которые энциклопедии.должны опираться.

Раздел «Главное значение корня»

1. Нигде в Википедии не определяется корень отрицательного порядка, да и в других источниках он мне ни разу не встречался (кому он нужен, непонятно). Выбросил.

Раздел «Логические основания»

1. Фраза о кватернионах дублирует уже имеющуюся информацию. Удалил.

Leonid G. Bunich / обс. 14:30, 8 мая 2021 (UTC)

Как по-честному объяснить читателю, почему для определения мнимой единицы интерес представляет именно ±2-я степень, а не другая чётная?

Этот вопрос чем-то похож на вопрос о том, почему для оценки рассеяния часто используют именно квадратичное отклонение.
К сожалению, я никак не могу нигде найти источники, чтобы дать ответ на эти вопросы. Но неужели просто так давать определение, что мнимая единица — это число, квадрат которого равен −1? А если читатель так и не найдёт человеческого объяснения того, почему люди так «зациклены» на вторых степенях? :<

Это как скалярное произведение, каким его изучают в школе (и, может быть, в вузах): по моему личному опыту, никто в школе так и не объяснил, почему в определении скалярного произведения используется именно косинус, чем он так интересен. Это лишь я сама из сторонних источников (каких оказалось мало) поняла, что смысл косинуса кроется в проецировании векторов. Причём с помощью этого наглядного определения можно, например, очень легко доказать дистрибутивность скалярного умножения, а вот если пользоваться только определением через косинус, то это, наоборот, трудно и невозможно запомнить.

Mylania⁽^-^⁾ (T, C) 03:20, 6 июня 2021 (UTC)

Если рассматривать в качестве нашей цели поле, в котором каждый многочлен имеет корни, то есть строить комплексное поле как поле разложения вещественного многочлена некоторой степени, то ответ простой: первой степени недостаточно, а вторая — в самый раз (многочлен $x^{2}+1$), так что рассматривать прочие варианты — пустая потеря времени. Думаю, именно по этой причине авторов учебников данный вопрос нимало не волнует. Leonid G. Bunich / обс. 10:22, 6 июня 2021 (UTC)

• Мне интересно было рассмотреть вашу версию ^^. И, я так поняла, поле разложения вещественного многочлена над $\mathbb {R} ,$ по сути, представляет собой $\mathbb {R} [x_{1},x_{2}\cdots x_{n}]=\{s+tx_{1}~|~s,t\in \mathbb {R} [x_{2},x_{3}\cdots x_{n}]\},$ где x₁, …, x_n — это все корни многочлена. И задача, о которой вы сказали, — это подобрать такой многочлен, чтобы ни один из его корней не был в $\mathbb {R}$ (надеюсь, я ничего не искажаю). Но в вашей версии меня кое-что настораживает, потому что она равносильна вот чему:

Допустим, наша цель — подобрать такое число n, чтобы полином xⁿ + 1 не имел корней из $\mathbb {R}$ [а имел какие-то другие корни, расширение поля $\mathbb {R}$ относительно которых и будем называть полем комплексных чисел $\mathbb {C}$]. Первая степень не подходит, а вторая — в самый раз, а значит, не стоит тратить время на остальные показатели. И, возможно, один из корней полученного уравнения (2-й степени) как раз и назовём мнимой единицей.

Проблема в том, что это как раз и вызывает тот самый вопрос, который я задала в этой теме. И читатель, скорее всего, будет задавать вопрос: неужели двойку выбрали просто как наименьшее положительное число, с помощью которого из вещественного числа можно получить невещественное?

Милания⁽^-^⁾ (О, В) 02:39, 7 июня 2021 (UTC)

Любой выбор чётного показателя корня не приводит к существенному расширению результирующего поля по сравнению с выбором двойки. Как говорили в старой рекламе, «Если нет разницы, зачем платить больше?» Leonid G. Bunich / обс. 13:34, 7 июня 2021 (UTC)

• Проблема в том, что не все знают, что извлечение корня целой (а потом и комплексной) ненулевой степени не расширит $\mathbb {C} .$ И получается вот что:

1. новичок не знает, почему именно ±2-я степень;
2. а ещё не знает, что́ произойдёт при извлечении корня из мнимого числа. Может, существует такой ненулевой показатель корня, при котором извлечение корня расширит $\mathbb {C}$?

Поэтому на первый вопрос надо искать другое объяснение. И самые понятные объяснения, до каких я только додумалась в своё время, — это через комплексное сопряжение и через тот факт, что благодаря определению мнимой единицы той, какая она есть, получается мультипликативность модуля. И вот именно с помощью этих двух фактов можно не только разрешить первый вопрос, но и доказать, что при умножении комплексных чисел аргументы складываются, а оттуда — формулу Муавра и разрешение второго вопроса.

Милания⁽^-^⁾ (О, В) 05:18, 8 июня 2021 (UTC)

• Знаете, мне кажется, что, чтобы читатель понял, почему выбрана именно ±2-я степень, можно хотя бы сказать, что сумма и произведение двух чисел могут быть вещественными одновременно, только если сами числа вещественны или если они сопряжены.
  • Мне кажется, что мой подход (мнимая единица как корень уравнения $x^{2}+1=0$) будет понятнее читателю, чем ваша довольно сложная цепочка взаимозависимостей. Тем более что совершенно аналогично при расширении натуральных чисел до целых вводятся понятие нуля (как корня уравнения $1+x=1$) и отрицательного числа $-n$ (как корня уравнения $n+x=0).$ Да и с источниками у моей версии проще. Leonid G. Bunich / обс. 17:04, 8 июня 2021 (UTC)

• Нет, очевидно, я не имею в виду, чтобы утверждение
  

${\begin{cases}a+b\in \mathbb {R} \\ab\in \mathbb {R} \\a\in \mathbb {C} \\b\in \mathbb {C} \end{cases}}\Leftrightarrow {\big [}a={\bar {b}}\in \mathbb {C} \lor [a\in \mathbb {R} \land b\in \mathbb {R} ]{\big ]}$
(в словесной форме)

было написано именно в преамбуле, где-то рядышком с определением мнимой единицы. Конечно же, я хочу, чтобы это находилось где-то в разделе про сопряжение, но хотя бы где-то находилось.

Милания⁽^-^⁾ (О, В) 00:40, 9 июня 2021 (UTC)

• И ещё: если человек, который только изучает $\mathbb {C} ,$ так и не поймёт, расширяет ли извлечение корня поле комплексных чисел, то он тем более так и не поймёт, почему же для мнимой единицы выбрана степень ±2. Вот почему я выше ответила вам:

Поэтому на первый вопрос надо искать другое объяснение

и обратила ваше внимание на ещё один вопрос, который находится выше под номером 2.

01:01, 9 июня 2021 (UTC)

Не могу сказать, что я до конца понял ваши рассуждения, но если найдёте АИ, то будет интересно ознакомиться. Leonid G. Bunich / обс. 15:11, 9 июня 2021 (UTC)

• Смысл моих последних реплик вот в чём: смотрите, вы предположили, что авторов АИ не волнует вопрос о показателе степени, с помощью которой задаётся определение мнимой единицы, потому, что извлечение корня не расширяет $\mathbb {C} ,$ а значит, на двойке можно остановиться. То есть вы высказали это мнение в предложении, что должно быть очевидно, что извлечение корня не расширяет $\mathbb {C} ,$ а оттуда должно стать очевидно, почему выбран показатель ±2.

При этом я пытаюсь объяснить, что это на самом деле для новичков и даже для средненьких может быть неочевидным (в отличие от сложения, вычитания и умножения — которые новичок может проверить руками, вольно-невольно перенося какие-то аксиомы из $\mathbb {R}$ на $\mathbb {C} \setminus \mathbb {R} ,$ — а потом, может быть, и деления — да и то даже оно уже становится неочевидно, пока не узнать все прелести сопряжённых чисел, — что уж говорить о корне!). (Насчёт формулы Муавра я объясню ниже.^^)

«И вдруг, — подумает новичок, — может быть, существует какая-то такая мнимая единица, ±4-я (±6-я, ±8-я…) степень которой равна −1, но которую невозможно выразить через $\mathbb {R} [i]=\{s+ti\mid s,t\in \mathbb {R} \},$ где i — это комплексная мнимая единица. Если есть, то, может, их тоже нужно выделить как какие-то другие мнимые единицы, которые расширяют $\mathbb {R} [i]$ и уделять внимание некоторым из каких имеет смысл? Но как же мне всё это выяснить?»

И вот жадный до знаний новичок обнаруживает ту самую формулу Абраама де Муавра, и она почти спасает его положение. Теперь остаётся только прочувствовать её доказательство, усвоить её почти как аксиому! Итак, что он видит в этой формуле? А видит он модуль и аргумент, определение которых он выясняет. Но теперь у него возникает ещё больше вопросов: «Почему модуль определяется как квадратный корень из суммы квадратов вещественной и мнимой части, где понятие мнимой части как раз связано с мнимой единицей, квадрат которой равен −1; и почему Re и Im изображают перпендикулярно? Чтобы специально подогнать под формулу?» Получается порочный круг (но он связан не с технической стороной доказательства, а с тем, чтобы осознать, присвоить доказательство, почувствовать его на «естественном уровне»).

Вот почему так важно объяснить, почему мнимую единицу определяют через ±2-ю степень, через свойства сопряжения или через мультипликативность модуля (и новичок поймёт их равносильность), а уже оттуда вывести аддитивность аргументов и формулу Муавра и наконец-то понять, что радикалы не расширяют $\mathbb {C} .$ А вот в обратную сторону из того факта, что радикалы не расширяют $\mathbb {C} ,$ выводить объяснение того, почему для мнимой единицы выбрана ±2-я степень, — это безнадёжный путь (и я объяснила почему начиная с 3-го абзаца).

Милания⁽^-^⁾ (О, В) 02:09, 10 июня 2021 (UTC)