Ладейный граф

Ладейный граф
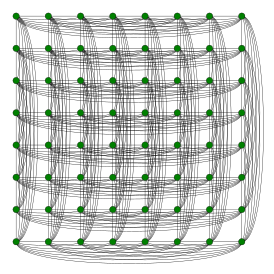Ладейный граф 8x8
Вершин	nm
Рёбер	nm(n + m)/2 - nm
Диаметр	2
Обхват	3 (если max(n,m) ≥ 3)
Хроматическое число	max(n, m)
Свойства	регулярный вершинно-транзитивный совершенный хорошо покрытый
Медиафайлы на Викискладе

В теории графов ладе́йным гра́фом называется граф, представляющий все допустимые ходы ладьи на шахматной доске — каждая вершина представляет клетку на доске, а рёбра представляют возможные ходы. Ладейные графы являются крайне симметричными совершенными графами — их можно описать в терминах числа треугольников, которым принадлежит ребро и существования цикла длины 4, включающего любые две несмежные вершины.

Определение

Ладейный граф n × m представляет допустимые ходы ладьи на доске n × m. Вершинам графа можно задать координаты (x,y), где 1 ≤ x ≤ n и 1 ≤ y ≤ m. Две вершины (x₁,y₁) и (x₂,y₂) смежны тогда и только тогда, когда либо x₁ = x₂, либо y₁ = y₂. То есть, если они лежат на одной и той же линии клеток (горизонтальной или вертикальной).

Для ладейного графа n × m общее число вершин равно nm. Для квадратной доски n × n число вершин ладейного графа равно $n^{2}$ и число рёбер равно $n^{3}-n^{2}$. В последнем случае граф известен как двумерный граф Хэмминга.

Ладейный граф на доске n × m можно определить как прямое произведение двух полных графов K_n $\square$ K_m. Дополнение ладейного графа 2 × n является короной.

Симметрия

Ладейные графы вершинно-транзитивны и (n + m − 2)-регулярны. Это единственный класс регулярных графов, который можно построить на основе ходов стандартных шахматных фигур. Если m ≠ n, симметрии ладейных графов образованы независимыми перестановками строк и столбцов графа. Если n = m, у графа появляются дополнительные симметрии, обменивающие строки и столбцы. Ладейный граф для квадратной шахматной доски является симметричным.

Любые две вершины ладейного графа находятся на расстоянии единица либо два, в зависимости от того, являются ли они смежными или нет. Любые две несмежные вершины можно перевести в любые две другие несмежные вершины с помощью симметрии графа. Если ладейный граф не квадратен, пары смежных вершин распадаются на две орбиты группы симметрий согласно их смежности — по горизонтали или по вертикали, но в случае квадратного графа любые две смежные вершины можно перевести из одной в другую с помощью симметрии и, таким образом, граф является дистанционно-транзитивным.

Если m и n взаимно просты, группа симметрий S_m×S_n ладейного графа содержит в качестве подгруппы циклическую группу C_mn = C_m×C_n, которая действует путём перестановки mn вершин циклически. Таким образом, в этом случае ладейный граф является циркулянтным.

Совершенство

3×3 ладейный граф, раскрашенный тремя цветами, в котором показана клика, имеющая три вершины. В этом графе и во всех его порождённых подграфах хроматическое число равно кликовому числу, так что он является совершенным.

Ладейный граф можно рассматривать как рёберный граф полного двудольного графа K_n,m. То есть, он имеет по вершине для каждого ребра K_n,m и две вершины ладейного графа смежны тогда и только тогда, когда соответствующие рёбра полного двудольного графа имеют общую вершину. С этой точки зрения ребро двудольного графа, соединяющее вершину i одной стороны с вершиной j другой стороны, соответствует клетке шахматной доски с координатами (i,j).

Любой двудольный граф является подграфом полного двудольного графа, а значит любой рёберный граф двудольнго графа является порождённым подграфом ладейного графа. Рёберные графы двудольных графов совершенны — в нём и в любом его порождённом подграфе число цветов, необходимых для любой раскраски вершин, равно числу вершин в наибольшей клике. Рёберные графы двудольных графов образуют важное семейство совершенных графов, одно из небольшого числа семейств, использованных Чудновской с соавторами для описания совершенных графов и для того, чтобы показать, что любой граф без нечётных дыр и антидыр совершенен. В частности, совершенны ладейные графы.

Поскольку ладейные графы совершенны, число цветов, которые нужны для раскраски графа, равно размеру наибольшей клики. Клики ладейного графа являются подмножествами его строк и столбцов и наибольшее из них имеет размер max(m,n), так что это число является хроматическим числом графа. n-цветную раскраску n×n ладейного графа можно рассматривать как латинский квадрат — он описывает способ заполнения строк и столбцов n×n решётки n различными значениями, при котором ни одно значение не появляется дважды в строках и столбцах.

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Расположение восьми ладей на шахматной доске так, что ладьи не бьют друг друга. Эти ладьи образуют максимальное независимое множество в соответствующем ладейном графе

Независимое множество в ладейном графе — это множество вершин, никакие две из которых не принадлежат одной строке или столбцу графа. В терминах шахмат это соответствует расположению ладей, никакие две из которых не атакуют друг друга. Совершенные графы можно также описать как графы, в которых для любого порождённого подграфа размер наибольшего независимого множества равен числу клик в разложении вершин графа на минимальное число клик. В ладейном графе множество строк или столбцов (какое из них меньше) образует такое оптимальное разложение. Размер наибольшего независимого множества равен, таким образом, min(m,n). Любая оптимальная раскраска в ладейном графе является максимальным независимым множеством.

Описание

Мун описывает ладейный граф m × n как единственный граф, имеющий следующие свойства:

• Он имеет mn вершин, каждая из которых инцидентна n + m − 2 рёбрам.
• mn(m −1)/2 рёбер принадлежат m − 2 треугольникам, а оставшиеся mn(n −1)/2 рёбер принадлежат n − 2 треугольникам.
• Любые две несмежные вершины принадлежат единственному циклу из 4 вершин.

Если n = m, эти условия можно упростить до утверждения, что ладейный граф n×n является сильно регулярным графом с параметрами srg(n², 2n − 2, n − 2, 2), и что любой сильно регулярный граф с такими параметрами должен быть ладейным графом n×n если n≠4. Если n=4, существует ещё один сильно регулярный граф, а именно, граф Шрикханде, который имеет такие же параметры, что и ладейный граф 4×4. Граф Шрикханде отличается от ладейного графа 4×4 тем, что окрестность любой вершины графа Шрикханде связана в цикл длины 6, в то время как в ладейном графе они принадлежат двум треугольникам.

Доминирование

Число доминирования графа — это минимальный размер множества среди всех доминирующих множеств. В ладейном графе множество вершин является доминирующим множеством тогда и только тогда, когда любая клетка доски либо принадлежат множеству, либо на один ход от элемента множества. Для доски m×n число доминирования равно min(m,n) .

Для ладейного графа k-доминирующее множество — это множество вершин, соответствующие клетки которых атакуют все остальные клетки (ходом ладьи) по меньшей мере k раз. k-кратное доминирующее множество для ладейного графа — это множество вершин, соответствующие клетки которых атакуют все остальные клетки (ходом ладьи) по меньшей мере k раз и атакуют свои же клетки не менее k − 1 раз. Минимальный размер среди всех k-доминирующих множеств и k-кратных доминирующих множеств — это k- доминирующее число и k-кратное доминирующее число, соответственно. На квадратной доске для чётных k k-доминирующее число равно nk/2 при n ≥ (k² − 2k)/4 и k < 2n. Аналогично k-кратное доминирующее число равно n(k + 1)/2 когда k нечётно и меньше чем 2n .

См. также

• Граф ходов короля
• Граф ходов коня
• Граф решётки

Литература

• Ján Beka. K_n-decomposition of the line graphs of complete bipartite graphs // Octogon Mathematical Magazine. — 2001. — Т. 9, вып. 1A. — С. 135–139.
• Bekmetjev, Airat; Hurlbert, Glenn (2004). "The pebbling threshold of the square of cliques". arXiv:math.CO/0406157. {{cite arXiv}}: |class= игнорируется (справка)
• Berger-Wolf, Tanya Y.; Harris, Mitchell A. (2003). "Sharp bounds for bandwidth of clique products". arXiv:cs.DM/0305051. {{cite arXiv}}: |class= игнорируется (справка)
• Paul Burchett, David Lane, Jason Lachniet. K-domination and k-tuple domination on the rook's graph and other results // Congressus Numerantium. — 2009. — Т. 199. — С. 187—204.
• Maria Chudnovsky, Neil Robertson, Paul Seymour, Robin Thomas. The strong perfect graph theorem // Annals of Mathematics. — 2006. — Т. 164, вып. 1. — С. 51—229. — doi:10.4007/annals.2006.164.51.
• Noam Elkies. Graph theory glossary. — 2004.
• A. J. Hoffman. On the line graph of the complete bipartite graph // Annals of Mathematical Statistics. — 1964. — Т. 35, вып. 2. — С. 883—885. — doi:10.1214/aoms/1177703593.
• van der Hofstad, Remco; Luczak, Malwina J. (2008). "Random subgraphs of the 2D Hamming graph: the supercritical phase". arXiv:0801.1607 [math.PR].
• Renu Laskar, Charles Wallis. Chessboard graphs, related designs, and domination parameters // Journal of Statistical Planning and Inference. — 1999. — Т. 76, вып. 1—2. — С. 285—294. — doi:10.1016/S0378-3758(98)00132-3.
• van der Hofstad, Remco; Luczak, Malwina J.; Spencer, Joel (2008). "The second largest component in the supercritical 2D Hamming graph". arXiv:0801.1608 [math.PR].
• G. MacGillivray, K. Seyffarth. Classes of line graphs with small cycle double covers // Australasian Journal of Combinatorics. — 2001. — Т. 24. — С. 91—114.
• J. W. Moon. On the line-graph of the complete bigraph // Annals of Mathematical Statistics. — 1963. — Т. 34, вып. 2. — С. 664—667. — doi:10.1214/aoms/1177704179.
• D. de Werra, A. Hertz. On perfectness of sums of graphs // Discrete Mathematics. — 1999. — Т. 195, вып. 1—3. — С. 93—101. — doi:10.1016/S0012-365X(98)00168-X.
• Яглом А. М., Яглом И. М. Неэлементарные задачи в элементарном изложении. — Dover, 1987.

Ссылки

• Weisstein, Eric W. Lattice Graph (англ.) на сайте Wolfram MathWorld.