Конечное правило подразделения

Перспективная проекция додекаэдрального замощения в H³. Заметьте рекурсивную структуру: каждый пятиугольник содержит меньшие пятиугольники, которые содержат меньшие пятиугольники. Это пример правил подразделения, получающегося из конечного пространства (т.е. замкнутого 3-многообразия).

В математике конечное правило подразделения — это рекурсивный способ деления многоугольника и других двумерных фигур на всё меньшие и меньшие части. Правила подразделения в этом смысле является обобщением фракталов. Вместо повторения одного и того же узора снова и снова здесь имеются небольшие изменения на каждом шаге, что позволяет получить более богатые структуры, сохраняя при этом поддержку элегантного стиля фракталов . Правила подразделения используются в архитектуре, биологии и информатике, а также при изучении гиперболических многообразий. Подстановки плиток являются хорошо изученным видом правил подразделения.

Определение

Правило подразделения берёт замощение на плоскости многоугольниками и превращает его в новое замощение путём деления каждого многоугольника на меньшие многоугольники. Правило конечно, если имеется лишь конечное число путей деления каждого многоугольника. Каждый способ деления плитки называется типом плитки. Каждый тип плитки представляется меткой (обычно — буквой). Каждый тип плитки делится на меньшие типы плиток. Каждое ребро также делится на конечное число типов рёбер. Конечные правила подразделения могут только делить плитки, которые состоят из многоугольников, помеченных типами плиток. Такие замощения называются комплексами подразделения для правила подразделения. Если задан какой-либо комплекс подразделения для правила подразделения, мы можем делить его снова и снова для получения последовательности замощений.

Например, бинарное подразделение имеет один тип плитки и один тип ребра:

Бинарное правило подразделения

Поскольку плитки являются только четырёхугольниками, бинарное подразделение может дать замощение, состоящее только из четырёхугольников. Это означает, что комплексы подразделения являются мозаиками из четырёхугольников. Мозаика может быть правильной, но не обязана быть:

Мы начинаем с комплекса с четырьмя четырёхугольниками и подразделяем их дважды. Все квадраты являются плитками типа A.

Здесь мы начинаем с четырёх четырёхугольников и подразделяем их дважды. Все квадраты являются плитками типа A.

Примеры конечных правил подразделения

Барицентрическое подразделение является примером правила подразделения с одним типом рёбер (которые подразделяются на два ребра) и одним типом плитки (треугольник, который подразделяется на 6 меньших треугольников). Любая триангулированная поверхность является комплексом барицентрического подразделения .

Мозаика Пенроуза может быть получена с помощью правила подразделения на наборе из четырёх типов плиток (кривые в таблице ниже только помогают показать, как плитки складываются вместе):

Название	Начальные плитки	Поколение 1	Поколение 2	Поколение 3
Полудельтоид
Полустрела
Солнце
Звезда

Некоторые рациональные отображения дают начало конечным правилам подразделения . Они включают большинство отображений Латте .

Любое простое неразделимое альтернирующее дополнение узла или зацепления имеет правило подразделения с некоторыми плитками, которые не подразделяются согласно границам дополнения зацепления . Правила подразделения показывают, как бы выглядело ночное небо, если бы кто-то жил в дополнении узла В этом случае вселенная заворачивается в себя (т.е. не односвязна), и наблюдатель видел бы видимую часть вселенной повторяющейся в бесконечной мозаике. Правило подразделения описывает эту мозаику.

Правило подразделения выглядит по-разному для различных геометрий. Вот правило подразделения для трилистника, который не является гиперболическим зацеплением:

Правило подразделения трилистника

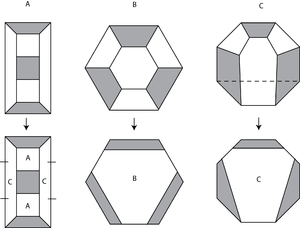
А вот правило подразделения для колец Борромео, которые гиперболичны:

Правило подразделения Борромео

В каждом случае правило подразделения действует на некоторое замощение сферы (т.е. ночного неба), но проще нарисовать малую часть звёздного неба, соответствующего отдельной плитке, многократно подразделяемой. Вот что происходит для трилистника:

Подразделения комплекса подразделения для дополнения трилистника.

И для колец Борромео:

Подразделения комплекса подразделения для дополнения колец Борромео.

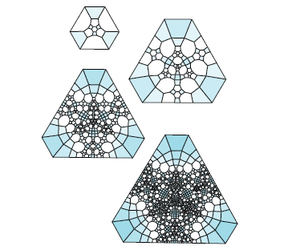
Правила подразделения в других размерностях

Правила подразделения можно обобщить на другие размерности . Например, барицентрическое подразделение применимо во всех размерностях. Бинарное подразделение также может быть обобщено на другие размерности (где гиперкубы делятся серединными гиперплоскостями), как в доказательстве леммы Гейне — Бореля.

Правило подразделения для четырёхмерного тора. Грани B плиток, подразделения которых касаются только C плиток и грани B плиток, не касающиеся A плиток.

Строгое определение

Конечное правило подразделения $R$ состоит из следующего .

1. Конечный 2-мерный CW-комплекс $S_{R}$, называемый комплексом подразделения, с фиксированной структурой ячеек, такой что $S_{R}$ является объединением замкнутых 2-ячеек. Мы предполагаем, что для каждой замкнутой 2-ячейки ${\tilde {s}}$ комплекса $S_{R}$ существует CW структура $s$ на замкнутых 2-дисках, такая, что $s$ имеет по меньшей мере две вершины, вершины и рёбра $s$ содержатся в $\partial s$, и характеристическое отображение $\psi _{s}:s\rightarrow S_{R}$, отображающее в ${\tilde {s}}$, ограничивается гомеоморфизмом в каждую открытую ячейку.

2. Конечный двухмерный CW-комплекс $R(S_{R})$, который является подразделением $S_{R}$.

3. Непрерывное отображение ячеек $\phi _{R}:R(S_{R})\rightarrow S_{R}$, называемое отображением подразделения, ограничение которого на каждую открытую ячейку является гомеоморфизмом.

Каждый CW-комплекс $s$ в вышеприведённом определении (с характеристическим отображением $\psi _{s}$) называется типом плитки.

$R$-комплекс для правила подразделения $R$ является двумерным CW-комплексом $X$, который является объединением замкнутых 2-ячеек, вместе с непрерывным отображением ячеек $f:X\rightarrow S_{R}$, ограничение которого на каждую открытую ячейку является гомеоморфизмом. Мы можем подразделить $X$в комплекс $R(X)$, потребовав, чтобы порождённое отображение $f:R(X)\rightarrow R(S_{R})$ ограничивалось гомеоморфизмом в каждую ограниченную ячейку. $R(X)$ снова $R$-комплекс с отображением $\phi _{R}\circ f:R(X)\rightarrow S_{R}$. Повторяя процесс, мы получим последовательность подразделённых $R$-комплексов $R^{n}(X)$ с отображениями $\phi _{R}^{n}\circ f:R^{n}(X)\rightarrow S_{R}$.

Бинарное подразделение является одним из примеров:

Бинарное правило подразделения.

Комплекс подразделения может быть создан склеиваем вместе противоположных рёбер квадрата, что превращает комплекс подразделения $S_{R}$ в тор. Отображение подразделения $\phi$ является удвоенным отображением тора, оборачивающим меридиан относительно себя дважды, и то же самое для широты. То есть это четырёхкратное накрытие. Плоскость, замощённая квадратами, является комплексом подразделения для этого правила подразделения со структурным отображением $f:\mathbb {R} ^{2}\rightarrow R(S_{R})$, заданным стандартным отображением накрытия. При подразделении каждый квадрат на плоскости подразделяется на квадраты в четверть размера.

Свойства квазиизометрии

Граф истории третьего шага правила подстановки.

Правила подразделения могут быть использованы для изучения свойств квазиизометрии некоторых поверхностей . Если задано правило подразделения $R$ и комплекс подразделения $X$, мы можем построить граф, называемый графом истории, в который заносятся действия правила подразделения. Граф состоит из двойственных графов каждого шага $R^{n}(X)$, вместе с рёбрами, соединяющими каждую плитку из $R^{n}(X)$ с её подразделениями в $R^{n+1}(X)$.

Свойства квазиизометрии графов истории можно изучать с помощью правил подразделения. Например, граф истории является квазиизометрией гиперболического пространства в точности тогда, когда правила подразделения являются конформными, как описано в комбинаторной теореме Римана об отображении.

Приложения

Пример правила подразделения, применяемого в иcламской культуре (мозаика гирих)

Первые три шага подразделения Кэтмула–Кларка куба для подразделения поверхности, показанной ниже.

Природа ветвления бронхов может быть смоделирована конечными правилами подразделения.

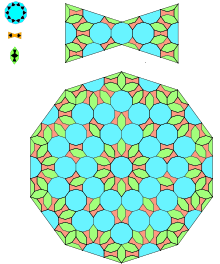
Мозаика Гирих в исламской архитектуре — самоподобное замощение, которое можно смоделировать конечными правилами подразделения . В 2007 Питер Лу из Гарвардского университета и профессор Пол Штейнхардт из Принстонского университета опубликовали статью в журнале Science с гипотезой, что эти мозаики обладают свойствами, согласующимися с самоподобными фрактальными квазикристальными замощениями, такими как мозаики Пенроуза (мозаика предложена в 1974), но мозаики гирих использовались пять столетий ранее.

Подразделенные поверхности в компьютерной графике использует правила подразделения для детализации поверхности до любого заданного уровня точности. На этих подразделениях поверхности (таких как подразделённая поверхность Кэтмелла — Кларка) берётся полигональная сетка (используемая для 3D-анимации в фильмах) и детализируется к сетке с большим числом многоугольников путём добавления и сдвига точек согласно различным рекурсивным формулам . Хотя много точек в этом процессе сдвигаются, каждая новая сетка комбинаторно является подразделением старой сетки (что означает, что для любого ребра и вершины старой сетки можно указать ребро и вершину новой сетки, плюс несколько добавочных рёбер и вершин).

Правила подразделения использовали Кэннон, Флойд и Парри (2000) для изучения структур растущих биологических организмов. Кэннон, Флойд и Парри разработали математическую модель роста, которая демонстрирует, что некоторые системы, определённые простыми конечными правилами подразделения, дают в результате объекты (в их случае, — ствол дерева), формы большого объёма у которых со временем колеблются широко, хотя локальные правила подразделения остаются теми же самыми. Кэннон, Флойд и Парри применили также свою модель к анализу роста тканей крыс. Они высказали предположение, что "отрицательно выгнутая" (или неевклидова) природа микроскопических структур роста биологических организмов является одой из ключевых причин, почему организмы в крупном масштабе не выглядят как кристаллы или многогранники, а, фактически, во многих случаях имеют сходство с самоподобными фракталами. В частности, они высказали предположение, что такая "отрицательно выгнутая" локальная структура проявляется в крайне складчатой и крайне связанной природе тканей мозга и лёгких.

Гипотеза Кэннона

Кэннон, Флойд и Парри первыми начали изучать конечные правила подразделения в попытке доказать следующую гипотезу:

Гипотеза Кэннона: Любая громовская гиперболическая группа с 2-сферой на бесконечности действует геометрически на гиперболическое 3-пространство .

Здесь геометрическое действие — это компактное, вполне разрывное действие изометрий. Гипотеза была частично решена Григорием Перельманом в его доказательстве гипотезы Тёрстона, которая утверждает (в частности), что любая громовская гиперболическая группа, являющаяся группой 3-многообразия, должна действовать геометрически в гиперболическом 3-пространстве. Однако остаётся показать, что громовская гиперболическая группа с 2-сферой на бесконечности является группой 3-многообразия.

Кэннон и Свенсон показали, что гиперболическая группа с 2-сферой на бесконечности имеет связанное с ней правило подразделения. Если это правило подразделения в определённом смысле конформно, группа будет группой 3-многообразия с геометрией гиперболического 3-пространства.

Комбинаторная теорема Римана об отображениях

Правила подразделения даёт последовательность замощений поверхности, а замощения дают идею расстояния, длины и площади (если считать, что каждая плитка имеет длину и площадь 1). В пределе расстояние, которое получается из этих замощений, может в некотором смысле сходиться к аналитической структуре на поверхности. Комбинаторная теорема Римана об отображениях даёт необходимое и достаточное условие, чтобы это произошло .

Для формулировки теоремы требуется некоторая подготовка. Замощение $T$ кольца $R$ даёт два инварианта, $M_{sup}(R,T)$ и $m_{inf}(R,T)$, называемых аппроксимирующими модулями. Они подобны классическому модулю кольца. Они определяются с помощью функций веса. Функция веса $\rho$ каждой плитке замощения $T$ сопоставляет неотрицательное число, называемое весом. Для любого пути в $R$ можно задать длину как сумму весов всех плиток в пути. Определим высоту $H(\rho )$ пути в $R$ по $\rho$ как инфимум длины всех возможных путей, соединяющих внутреннюю границу $R$ со внешней границей. Длина окружности $C(\rho )$ круга $R$ по $\rho$ — это инфимум длины всех возможных путей, образующих цикл в кольце (т.е. не гомотопных нулю в R). Площадь$A(\rho )$ кольца $R$ по $\rho$ определяется как сумма квадратов всех весов в $R$. Теперь определим

$M_{sup}(R,T)=\sup {\frac {H(\rho )^{2}}{A(\rho )}}$

$m_{inf}(R,T)=\inf {\frac {A(\rho )}{C(\rho )^{2}}}$.

Заметим, что эти величины инвариантны при масштабировании метрики.

Последовательность $T_{1},T_{2},...$ плиток является конформным ($K$), если величина ячеек стремится к 0 и:

1. Для всех колец $R$ аппроксимирующие модули $M_{sup}(R,T_{i})$ и $m_{inf}(R,T_{i})$ для всех достаточно больших $i$ лежат в одном интервале вида $[r,Kr]$
2. Если задана точка $x$ на поверхности, окрестность $N$ точки $x$ и целое число $I$, то существует кольцо $R$ в $N\setminus \{x\}$, отделяющее x от дополнения $N$, так что с некоторого $i$ аппроксимирующие модули кольца $R$ больше числа $I$ .

Утверждение теоремы

Если последовательность $T_{1},T_{2},...$ плиток на поверхности является конформной ($K$) в вышеописанном смысле, то существует конформная структура на поверхности и константа $K'$, зависящая только от $K$, для которых классические модули и аппроксимирующие модули (для $T_{i}$ при достаточно большом $i$) любого заданного кольца $K'$-сопоставимы, что означает, что они лежат в одном интервале $[r,K'r]$.

Следствия

Из комбинаторной теоремы Римана об отображениях вытекает, что группа $G$ действует геометрически на $\mathbb {H} ^{3}$ тогда и только тогда, когда группа является громовской гиперболической, имеет сферу на бесконечности и естественные правила подразделения на сфере дают последовательность мозаик, которые конформны в описанном выше смысле. Таким образом, гипотеза Кэннона будет верна, если все такие правила подразделения конформны.

Литература

• B. Rushton. A finite subdivision rule for the n-dimensional torus // Geometriae Dedicata. — 2012. — Т. 167. — С. 23–34. — doi:10.1007/s10711-012-9802-5.
• Peter J Lu. Decagonal and quasi-crystalline tilings in medieval islamic architecture // Science. — 2007. — Т. 315. — С. 1106–1110. — doi:10.1126/science.1135491. — . — PMID 17322056.
• Peter J. Lu, Paul J. Steinhardt. Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture // Science. — 2007. — Т. 315, вып. 5815. — С. 1106–1110. — doi:10.1126/science.1135491. — . — PMID 17322056.
• J. W. Cannon, W. J. Floyd, W. R. Parry. Finite subdivision rules // Conformal Geometry and Dynamics. — 2001. — Т. 5.
• J. W. Cannon, W. J. Floyd, W. R. Parry. Constructing subdivision rules from rational maps // Conformal Geometry and Dynamics. — 2007. — Т. 11.
• J. W. Cannon, W. J. Floyd, W. R. Parry. Lattès maps and subdivision rules // Conformal Geometry and Dynamics. — 2010. — Т. 14.
• J. W. Cannon, W. J. Floyd, W. R. Parry. Pattern Formation in Biology, Vision and Dynamics. — World Scientific, 2000. — ISBN 981-02-3792-8, 978-981-02-3792-9..
• B. Rushton. Constructing subdivision rules from alternating links // Conform. Geom.. — 2010. — Вып. 14.
• James W. Cannon. The combinatorial Riemann mapping theorem // Acta Mathematica. — 1994. — Т. 173, вып. 2.
• J. W. Cannon, E. L. Swenson. Recognizing constant curvature discrete groups in dimension 3 // Transactions of the American Mathematical Society. — 1998. — Т. 350, вып. 2.
• D. Zorin. Subdivisions on arbitrary meshes: algorithms and theory. — Institute of Mathematical Sciences (Singapore), 2006. — (Lecture Notes Series).

Ссылки

• Bill Floyd's research page. This page contains most of the research papers by Cannon, Floyd and Parry on subdivision rules, as well as a gallery of subdivision rules.