Квантовый граф

Квантовый граф — граф, в котором каждому ребру назначена длина и на каждом ребре задано дифференциальное или псевдодифференциальное уравнение.

В качестве примера может служить электрическая сеть, состоящая из проводов (рёбер), соединённых в трансформаторных подстанциях (вершинах). Дифференциальные уравнения описывают напряжение на проводах, а граничные условия на вершинах обеспечивают нулевую сумму тока на всех входящих и исходящих ребрах каждой вершины.

Впервые были применены Лайнусом Полингом в 1930-е годы для моделирования свободных электронов в органических молекулах. Впоследствии нашли широкое применение в физике: в моделях систем квантового хаоса, при изучении волноводов, для моделирования перехода Андерсона в фотонных кристаллах; в мезоскопической физике квантовые графы используются для теоретического обоснования нанотехнологии. Более простое понятие квантовых графов было предложено Фридманом и другими..

Помимо решения дифференциальных уравнений на квантовом графе для конкретных приложений, изучаются вопросы управляемости (какое входное воздействие обеспечивает переход системы в желаемое состояние, например, для обеспечения достаточной электрической мощности на всех подстанциях) и идентификации систем (как и где необходимо провести измерения какой-либо величины, чтобы получить необходимую информацию о состоянии системы, например, измерение давления в водопроводной системе, чтобы обнаружить утечку воды).

Метрические графы

Метрический граф с тремя открытыми рёбрами, реализованный на плоскости. Пунктирные линии обозначают метрическое расстояние между двумя точками $x$ и $y$.

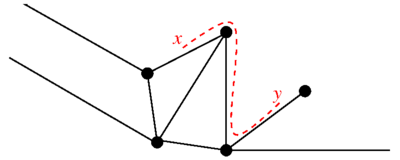
Метрический граф — граф, состоящий из множества вершин $V$ и множества рёбер $E$, где каждому ребру $e=(v_{1},v_{2})\in E$ поставлен в соответствие интервал $[0,L_{e}]$ так, что $x_{e}$ — координата на этом интервале, вершины $v_{1}$ и $v_{2}$ соответствуют $x_{e}=0$ и $x_{e}=L_{e}$, или наоборот. Выбор того, какая вершина соответствует нулевой координате, произволен, и переназначение вершин начала и конца ребра требует только замены координат ребра. Граф обладает естественной метрикой: для двух точек $x,y$ на графе, расстояние $\rho (x,y)$ — длина кратчайшего пути между ними, где длина пути измеряется как сумма длин ребёр пути.

Если в комбинаторном (классическом) графе ребро всегда соединяет пару вершин, то в квантовом графе допускаются полубесконечные ребра (лучи), таким рёбрам ставится в соответствие интервал $[0,\infty )$, где единственная вершина соответствует $x_{e}=0$. Граф, имеющий хотя бы одно такое ребро, называется открытым.

Квантовые графы

Квантовый граф — метрический граф с заданным дифференциальным (или псевдодифференциальным) оператором, действующим на функциях на рёбрах графа. Функция $f$ на метрическом графе определяется как $|E|$-кортеж функций $f_{e}(x_{e})$ на интервалах на рёбрах. Гильбертово пространство графа — $\bigoplus _{e\in E}L^{2}([0,L_{e}])$, где внутреннее произведение двух функций задано как

$\langle f,g\rangle =\sum _{e\in E}\int _{0}^{L_{e}}{\overline {f_{e}(x_{e})}}g_{e}(x_{e})\,dx_{e},$

$L_{e}$ может быть бесконечным в случае открытых рёбер. Простейший пример оператора на метрическом графе — оператор Лапласа. Оператор на ребре — это $-{\frac {{\textrm {d}}^{2}}{{\textrm {d}}x_{e}^{2}}}$, где $x_{e}$ — координата ребра. Для обеспечения самосопряжённости оператора необходимо подобрать подходящую область значений, обычно для этого выбирается пространство Соболева $H^{2}$ функций на рёбрах графа и соответствующие граничные условия на вершинах.

Простейший пример условий, обеспечивающих самосопряженность — граничные условия Дирихле $f_{e}(0)=f_{e}(L_{e})=0$ для каждого ребра. Собственные функции на конечных рёбрах могут быть записаны как:

$f_{e}(x_{e})=\sin \left({\frac {n\pi x_{e}}{L_{e}}}\right)$

для целого $n$. Если в графе нет открытых рёбер и длины рёбер несоизмеримы над рациональными числами, тогда носитель собственной функции лежит на одном ребре графа, и собственные значения равны ${\frac {n^{2}\pi ^{2}}{L_{e}^{2}}}$. Условия Дирихле не позволяют учитывать взаимодействие между интервалами на ребрах, так что спектр такой же, что и на множестве независимых (несоединённых) рёбер.

Более интересными самосопряжёнными граничными условиями, позволяющими учитывать взаимодействие между рёбрами, являются граничные условия Неймана или естественные граничные условия. Функция $f$ в области определения оператора непрерывна всюду на графе и сумма исходящих производных в каждой вершине равна нулю:

$\sum _{e\sim v}f'(v)=0$,

где $f'(v)=f'(0)$, если вершина $v$ соответствует $x=0$, и $f'(v)=-f'(L_{e})$, если $v$ соответствует $x=L_{e}$.

Также изучены свойства других операторов на метрических графах, например, более общий класс операторов Шрёдингера:

$\left(i{\frac {\textrm {d}}{{\textrm {d}}x_{e}}}+A_{e}(x_{e})\right)^{2}+V_{e}(x_{e})$,

где $A_{e}$ — «магнитный векторный потенциал» на ребре, $V_{e}$ — скалярный потенциал.

Другим примером является оператор Дирака на графе, который является матричным оператором, действующим на вектор-функциях, описывающих квантовую механику частиц с собственным моментом импульса равным $1/2$ (например, электрон). Оператор Дирихле — фон Неймана на графе — псевдодифференциальный оператор, который возникает при изучении фотонных кристаллов.

Основные результаты

Все самосопряженные граничные условия оператора Лапласа на графе можно классифицировать по схеме Кострикина и Шрадера. На практике, часто удобнее использовать предложенный Кучментом в 2004 году формализм, который позволяет сразу получить оператор в вариационной форме.

Пусть $v$ это вершина с $d$ выходящими рёбрами. Для удобства выберем координаты на рёбрах так, чтобы $v$ соответствовала $x_{e}=0$ для каждого ребра инцидентного $v$. Для функции $f$ на графе:

$\mathbf {f} =(f_{e_{1}}(0),f_{e_{2}}(0),\dots ,f_{e_{d}}(0))^{T},\qquad \mathbf {f} '=(f'_{e_{1}}(0),f'_{e_{2}}(0),\dots ,f'_{e_{d}}(0))^{T}$,

граничные условия на $v$ могут быть заданы парой матриц $A$ и $B$ с помощью матричного уравнения:

$A\mathbf {f} +B\mathbf {f} '=\mathbf {0}$.

Граничные условия задают самосопряжённый оператор, если $(A,B)$ имеет максимальный ранг $d$ и $AB^{*}=BA^{*}$.

Спектр оператора Лапласа на конечном графе может быть описан с помощью матрицы рассеивания.

Собственные значения на ребре заданы:

$-{\frac {d^{2}}{dx_{e}^{2}}}f_{e}(x_{e})=k^{2}f_{e}(x_{e}).\,$

Решение на ребре может быть представлено линейной комбинацией плоских волн.

$f_{e}(x_{e})=c_{e}{\textrm {e}}^{ikx_{e}}+{\hat {c}}_{e}{\textrm {e}}^{-ikx_{e}}$,

где в нестационарном уравнении Шрёдингера $c$ — коэффициент выходящей плоской волны в $0$, ${\hat {c}}$ — коэффициент входящей плоской волны в $0$. Граничные условия на $v$ определяют матрицу рассеивания:

$S(k)=-(A+ikB)^{-1}(A-ikB)$

Матрица рассеивания устанавливает отношение между векторами коэффициентов входящих и выходящих плоских волн на $v$, $\mathbf {c} =S(k){\hat {\mathbf {c} }}$. Для самосопряжённых граничных условий матрица $S$ унитарна. Элемент $\sigma _{(uv)(vw)}$ матрицы $S$ есть комплексная амплитуда перехода из направленного ребра $(uv)$ на ребро $(vw)$, которое в общем случае зависит от $k$. Однако для большого класса граничных условий матрица $S$ независима от $k$. Например, с граничными условиями Неймана

$A=\left({\begin{array}{ccccc}1&-1&0&0&\dots \\0&1&-1&0&\dots \\&&\ddots &\ddots &\\0&\dots &0&1&-1\\0&\dots &0&0&0\\\end{array}}\right),\quad B=\left({\begin{array}{cccc}0&0&\dots &0\\\vdots &\vdots &&\vdots \\0&0&\dots &0\\1&1&\dots &1\\\end{array}}\right).$,

подстановка $A$ и $B$ в уравнение (1) для $S$ даёт независимые от $k$ уравнения для амплитуд переходов

$\sigma _{(uv)(vw)}={\frac {2}{d}}-\delta _{uw}.\,$

где $\delta _{uw}$ — дельта функция Кронекера. По уравнениям для амплитуд переходов можно задать $2|E|\times 2|E|$ матрицу

$U_{(uv)(lm)}(k)=\delta _{vl}\sigma _{(uv)(vm)}(k){\textrm {e}}^{ikL_{(uv)}}.\,$

Матрицу $U$ называют матрицой рассеяния на рёбрах и её можно представлять себе как оператор квантовой эволюции на графе. $U$ унитарный оператор и действует на векторе $2|E|$ коэффициентов плоских волн для графа, где $c_{(uv)}$ — коэффициент плоской волны, переходящей с $u$ на $v$. При распространении плоской волны от вершины $u$ к вершине $v$, она получает фазу, равную ${\textrm {e}}^{ikL_{(uv)}}$.

Условие квантования: Собственная функция на графе может быть определена через её $2|E|$ соответствующих коэффициентов плоских волн. Так как собственная функция стационарна при квантовой эволюции, условие квантования для графа может быть описано используя оператор эволюции

$|U(k)-I|=0.\,$

Собственные значения $k_{j}$ возникают при таких $k$, при которых матрица $U(k)$ имеет собственное значение равное единице. Упорядочим спектр $0\leqslant k_{0}\leqslant k_{1}\leqslant \dots$.

Первая формула следа для графа была выведена Ротом (1983). В 1997 Коттос и Смилански использовали условие квантования, приведенное выше, чтобы получить следующую формулу следа для оператора Лапласа на графе, когда амплитуды переходов независимы от $k$. Формула следа устанавливает связь между спектором и периодическими орбитами графа.

$d(k):=\sum _{j=0}^{\infty }\delta (k-k_{j})={\frac {L}{\pi }}+{\frac {1}{\pi }}\sum _{p}{\frac {L_{p}}{r_{p}}}A_{p}\cos(kL_{p}).$

$d(k)$ называется плотностью состояний. Правая часть формулы состоит из двух частей: гладкая часть (часть Вейля) ${\frac {L}{\pi }}$ — среднее разделяющее собственных значений, и осциллирующая часть — сумма по всем периодическим орбитам $p=(e_{1},e_{2},\dots ,e_{n})$ на графе. $L_{p}=\sum _{e\in p}L_{e}$ — длина орбиты и $L=\sum _{e\in E}L_{e}$ — полная длина графа. Для орбиты, порождённой повторением более короткой примитивной орбиты, $r_{p}$ считает число перераспределений. $A_{p}=\sigma _{e_{1}e_{2}}\sigma _{e_{2}e_{3}}\dots \sigma _{e_{n}e_{1}}$ произведение амплитуд переходов в вершинах графа на орбите.

Приложения

Молекула нафталина

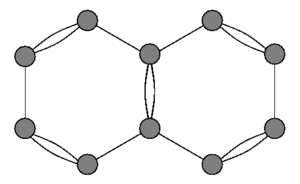
Квантовые графы были впервые использованы Полингом для моделирования спектра свободных электронов в таких органических молекулах как нафталин ещё в 1930-х годах. В первом приближении атомы моделируются вершинами, а $\sigma$-электроны — ребрами, которые описывают структуру молекулы, к которой привязаны электроны.

Сходная проблема возникает при изучении квантовых волноводов, являющихся мезоскопическими системами — системами, размеры которых исчисляются в нанометрах. Квантовый волновод может быть представлен как утолщённый граф, в котором рёбра — тонкие трубки. Спектр оператора Лапласа на таком волноводе, при выполнении некоторых условий, сходится к спектру оператора Лапласа на графе. Понимание мезоскопических систем играет важную роль в области нанотехнологий.

В 1997 году было предложено использовать квантовые графы в качестве моделей при изучении квантового хаоса. Классическое движение на графе может быть определено как вероятностная цепь Маркова, где вероятность рассеивания от ребра $e$ к ребру $f$ равна абсолютной величине квадрата амплитуды квантового перехода $|\sigma _{ef}|^{2}$. Для почти всех конечных связных квантовых графов вероятностная динамика эргодична и является перемешивающей, другими словами она хаотична.

Квантовые графы, вложенные в 2- или 3-мерное пространство, возникают при изучении фотонных кристаллов. В двумерном пространстве простая модель фотонного кристалла состоит из многоугольных клеток плотного диэлектрика с узкими переходами между клетками, заполненными воздухом. Изучение основных состояний диэлектриков приводит к псевдодифференциальным операторам на графе, который соответствует узким переходам.

Периодические квантовые графы, такие как, например, решётка в $\mathbb {R} ^{2}$, используются в качестве моделей для периодических систем^{[уточнить]}. Также квантовые графы были использованы для изучения феномена перехода Андерсона, где локализованные состояния возникают на рёбрах спектральных полос при наличии неупорядоченности.

Литература

• Analysis on graphs and its applications: Isaac Newton Institute for Mathematical Sciences, Cambridge, UK, January 8-June 29, 2007. — Providence, R.I.: American Mathematical Society, 2008. — xiii, 705 pages с. — ISBN 978-0-8218-4471-7, 0-8218-4471-7.
• Jens Bolte and Sebastian Endres Trace formulae for quantum graphs Архивная копия от 31 августа 2021 на Wayback Machine, стр. 247
• J. M. Harrison Quantum graphs with spin Hamiltonians Архивная копия от 31 августа 2021 на Wayback Machine, стр. 261
• J. P. Keating Quantum graphs and quantum chaos, стр. 279
• Peter Kuchment Quantum graphs: an introduction and a brief survey Архивная копия от 31 августа 2021 на Wayback Machine, стр. 291
• Freedman, Michael; Lovász, László; Schrijver, Alexander (2007). "Reflection positivity, rank connectivity, and homomorphism of graphs". Journal of the American Mathematical Society. 20 (01): 37—52. arXiv:math/0404468. doi:10.1090/S0894-0347-06-00529-7. ISSN 0894-0347. MR 2257396.