Алгоритм Франк — Вульфа
Алгоритм Франк — Вульфа[1] — это итеративный алгоритм оптимизации первого порядка[англ.] для выпуклой оптимизации с ограничениями[англ.]. Алгоритм известен также как метод условного градиента[2], метод приведённого градиента и алгоритм выпуклых комбинаций. Метод первоначально предложили Маргарита Франк[англ.] и Филип Вульф[англ.] в 1956[3]. На каждой итерации алгоритм Франк — Вульфа рассматривает линейное приближение целевой функции и движется в направлении минимизации этой линейной функции (на том же множестве допустимых решений).
Формулировка задачи[править | править код]
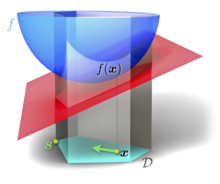
Предположим, что является компактным выпуклым множеством в векторном пространстве, а является выпуклой, дифференцируемой вещественнозначной функцией. Алгоритм Франк — Вульфа решает задачу оптимизации
- Минимизировать
- при условии .
Алгоритм[править | править код]
- Инициализация: Пусть и пусть будет точкой в .
- Шаг 1. Подзадача поиска направления: Находим , решающее задачу
- Минимизировать
- при условиях
- (Интерпретация: Минимизируем линейное приближение задачи, полученное аппроксимацией Тейлора первого порядка функции около .)
- Шаг 2. Определение размера шага: Положим , или, альтернативно, находим , минимизирующее при условии .
- Шаг 3. Пересчёт: Положим , и переходим к шагу 1.
Свойства[править | править код]
В то время как конкурирующие методы, такие как градиентный спуск для оптимизации с ограничениями, требуют на каждой итерации шага проецирования в множество допустимых значений, для алгоритма Франк — Вульфа нужно на каждой итерации лишь решить задачу линейного программирования на том же самом множестве, так что решение всегда остаётся принадлежащим множеству допустимых решений.
Сходимость алгоритма Франк — Вульфа в общем случае сублинейна — ошибка целевой функции по отношению к оптимальному значению равна после k итераций при условии, что градиент непрерывен по Липшицу по некоторой норме. Та же самая сходимость может быть показана, если подзадачи решаются лишь приближённо[4].
Итерации алгоритма могут быт всегда представлены как неплотная выпуклая комбинация экстремальных точек множества допустимых решений, что помогло популярности алгоритма для задач разрежённой жадной оптимизации в машинном обучении и обработки сигналов[5], а также для нахождения потоков минимальной стоимости в транспортных сетях[6].
Если множество допустимых решений задаётся набором линейных неравенств, то подзадача, решаемая на каждой итерации, становится задачей линейного программирования.
Хотя скорость сходимости в худшем случае для общего случая не может быть улучшена, более высокая скорость сходимости может быть получена для специальных задач, таких как строго выпуклые задачи[7].
Нижние границы на значение решения и прямо-двойственный анализ[править | править код]
Поскольку функция выпукла, для любых двух точек имеем:
Это выполняется также для (неизвестного) оптимального решения . То есть . Лучшая нижняя граница с учётом точки задаётся формулой
Эта последняя задача решается на каждой итерации алгоритма Франк — Вульфа, поэтому решение подзадачи нахождения направления на -й итерации может быть использовано для определения возрастающих нижних границ на каждой итерации путём присвоения и
Такие нижние границы на неизвестное оптимальное значение на практике очень важны, поскольку могут быть использованы как критерий остановки алгоритма и дают эффективный показатель качества приближения на каждой итерации, поскольку всегда .
Было показано, что разрыв двойственности, являющийся разницей между и нижней границей , уменьшается с той же скоростью, то есть
Примечания[править | править код]
- ↑ Алгоритм разработали Маргарита Франк и Филип Вульф, так что широко распространённое в русской литературе название Алгоритм Франка — Вульфа является ошибочным.
- ↑ Левитин, Поляк, 1966, с. 787-823.
- ↑ Frank, Wolfe, 1956, с. 95–110.
- ↑ Dunn, Harshbarger, 1978, с. 432.
- ↑ Clarkson, 2010, с. 1–30.
- ↑ Fukushima, 1984, с. 169–177.
- ↑ Bertsekas, 1999, с. 215.
Литература[править | править код]
- Левитин Е.С., Поляк Б.Т. Методы минимизации при наличии ограничений // Ж. вычисл. матем. и матем. физ.. — 1966. — Т. 6, вып. 5. — doi:10.1016/0041-5553(66)90114-5.
- Frank M., Wolfe P. An algorithm for quadratic programming // Naval Research Logistics Quarterly. — 1956. — Т. 3, вып. 1–2. — С. 95–110. — doi:10.1002/nav.3800030109.
- Dunn J. C., Harshbarger S. Conditional gradient algorithms with open loop step size rules // Journal of Mathematical Analysis and Applications. — 1978. — Т. 62, вып. 2. — С. 432. — doi:10.1016/0022-247X(78)90137-3.
- Clarkson K. L. Coresets, sparse greedy approximation, and the Frank-Wolfe algorithm // ACM Transactions on Algorithms. — 2010. — Т. 6, вып. 4. — С. 1–30. — doi:10.1145/1824777.1824783.
- A modified Frank-Wolfe algorithm for solving the traffic assignment problem // Transportation Research Part B: Methodological. — 1984. — Т. 18, вып. 2. — doi:10.1016/0191-2615(84)90029-8.
- Dimitri Bertsekas. Nonlinear Programming. — Athena Scientific, 1999. — С. 215. — ISBN 978-1-886529-00-7.
- Martin Jaggi. Revisiting Frank–Wolfe: Projection-Free Sparse Convex Optimization // Journal of Machine Learning Research: Workshop and Conference Proceedings. — 2013. — Т. 28, вып. 1. — С. 427–435. (Обзорная статья)
- Описание алгоритма Франк – Вульфа
- Jorge Nocedal, Stephen J. Wright. Numerical Optimization. — 2nd. — Berlin, New York: Springer-Verlag, 2006. — ISBN 978-0-387-30303-1.
- Fukushima, M. (1984). "A modified Frank-Wolfe algorithm for solving the traffic assignment problem". Transportation Research Part B: Methodological. 18 (2): 169—177. doi:10.1016/0191-2615(84)90029-8.
Ссылка[править | править код]
См. также[править | править код]
Для улучшения этой статьи желательно:
|






























